Docs
Notes
SI
Wertekontinuierliche Nichtlineare Systeme
Berechnung der Momente (UKF)

Berechnung der Momente: Unscented Kalman Filter (UKF)

Analytische Momente

  • Scheinbar die beste Methode, da schnell & feste Laufzeit 👍
  • Aber
    • Herleitung aufwändig
    • Formeln werden schnell unhandlich groß

Beispiel: Kubisches Sensorproblem (skalar)

Output yy ist nonlinear abhängig von dem Zustand xx:

y=h(x)+v=x3+v y=h(x)+v=x^{3}+v

Gegeben

  • Priore Schätzung xp∼N(x^p,σp2)x_p \sim \mathcal{N}(\hat{x}_p, \sigma_p^2)
  • Messung y^\hat{y}
  • Rauschen vv ist Gaußverteilt mit E{v}=0,Cov⁡{v}=Zv2E\{v\}=0, \operatorname{Cov}\{v\}=Z_{v}^{2}

Definiere

z:=[xy]⇒E{z‾}=[x^pE{h(x)}] z := \left[\begin{array}{l} x \\ y \end{array}\right] \Rightarrow E\{\underline{z}\}=\left[\begin{array}{c} \hat{x}_{p} \\ E\{h(x)\} \end{array}\right]

mit

E{h(x)}=∫Rh(x)fp(x)dx=∫Rx3fp(x)dx=x^p2+3x^pσp2=:E3 E\{h(x)\}=\int_{\mathbb{R}} h(x) f_{p}(x) d x=\int_{\mathbb{R}} x^{3} f_{p}(x) d x=\hat{x}_{p}^{2}+3 \hat{x}_{p} \sigma_{p}^{2}=:E_{3}

Definiere

hˉ(x)=h(x)−E{h(x)} \bar{h}(x)=h(x)-E\{h(x)\}

Dann

Cov⁡{z‾}=[CxxCxyCyxCyy]=[σp2E{(x−x^p)hˉ(x)}E{(x−x^p)hˉ(x)}E{h‾2(x)}+σv2] \operatorname{Cov}\{\underline{z}\}=\left[\begin{array}{ll} \mathbf{C}_{x x} & \mathbf{C}_{x y} \\ \mathbf{C}_{y x} & \mathbf{C}_{y y} \end{array}\right]=\left[\begin{array}{cc} \sigma_{p}^{2} & E\left\{\left(x-\hat{x}_{p}\right) \bar{h}(x)\right\} \\ E\left\{\left(x-\hat{x}_{p}\right) \bar{h}(x)\right\} & E\left\{\overline{h}^{2}(x)\right\}+\sigma_{v}^{2} \end{array}\right] E{(x−x^p)hˉ(x)}=E{(x−x^p)(x3−E3)}=E{x4−x^px3−E3x+x^pE3}=E4−x^pE3−E3x^p+x^pE3=E4−x^pE3 \begin{aligned} E\left\{\left(x-\hat{x}_{p}\right)\bar{h}(x)\right\} &= E\left\{\left(x-\hat{x}_{p}\right)\left(x^{3}-E_{3}\right)\right\} \\ &= E\left\{x^{4}-\hat{x}_{p} x^{3}-E_{3} x+\hat{x}_{p} E_{3}\right\} \\ &= E_4 - \hat{x}_p E_3 - E_3 \hat{x}_p + \hat{x}_p E_3 \\ &= E_4 - \hat{x}_p E_3 \end{aligned}

mit

Eq=x^p4+6x^p2σp2+3σp4=x^p4+6x^p22p2+3σp4−x^p4−3x^p2σp2=3σp4+3x^p2σp2=3σp2(x^p2+2p2) \begin{aligned} E_{q}&=\hat{x}_{p}^{4}+6 \hat{x}_{p}^{2} \sigma_{p}^{2}+3\sigma_{p}^{4} \\\\ &=\hat{x}_{p}^{4}+6 \hat{x}_{p}^{2} 2_{p}^{2}+3\sigma_{p}^{4}-\hat{x}_{p}^{4}-3 \hat{x}_{p}^{2} \sigma_{p}^{2} \\\\ &=3 \sigma_{p}^{4}+3 \hat{x}_{p}^{2} \sigma_{p}^{2} \\\\ &=3\sigma_{p}^{2}\left(\hat{x}_{p}^{2}+2_{p}^{2}\right) \end{aligned}

und

E{hˉ2(x)}=9x^p4σp2+36x^p2σp4+15σp6 E\left\{\bar{h}^{2}(x)\right\}=9 \hat{x}_{p}^{4} \sigma_{p}^{2}+36 \hat{x}_{p}^{2} \sigma_{p}^{4}+15\sigma_{p}^{6}

In der Kalmanfilter Filterungsgleichung einsetzen ergibt sich

x^e=x^p+CxyCyy−1(y^−E{h(x)})=skalarx^p+CxyCyy(y^−E{h(x)})σy2=σp2−CxyCyy−1Cyx=skalarσp2−Cxy2Cyy \begin{array}{l} \hat{x}_{e}=\hat{x}_{p}+\mathbf{C}_{xy}\mathbf{C}_{yy}^{-1}(\hat{y}-E\{h(x)\}) \overset{\text{skalar}}{=} \hat{x}_{p}+\frac{\mathbf{C}_{x y}}{\mathbf{C}_{y y}}(\hat{y}-E\{h(x)\}) \\ \sigma_{y}^{2}= \sigma_{p}^{2}-\mathbf{C}_{xy}\mathbf{C}_{yy}^{-1}\mathbf{C}_{yx} \overset{\text{skalar}}{=} \sigma_{p}^{2}-\frac{\mathbf{C}_{x y}^{2}}{\mathbf{C}_{y y}} \end{array}

Einschub: Momente Gaußdichte

Theorem

Die zentralen Momente einer Gaußdichte sind gegeben durch

$$ C\_{i}=E\_{f}\left\\{(\boldsymbol{x}-\hat{x})^{i}\right\\}=\left\\{\begin{array}{ll} \displaystyle\prod\_{j=1, j\text{ ungeradde}}^{i-1} j \sigma^{i}=1 \cdot 3 \cdot 5 \cdots(i-1) \sigma^{i} & i \text { gerade } \\\\ 0 & i \text { ungerade } \end{array}\right. $$

截屏2022-07-12 16.27.43

Numerische Momente

  • Verwendung von Standardverfahren zur Integration

  • 👍 Vorteile

    • Nutzung schneller Implementierungen
    • Einstellbare Genauigkeit
    • Adaptive Integration

  • 👎 Nachteile

    • Nicht für das konkrete Probleme der Momentenberechnung maßgeschneidert

Basierend auf Abtastwerten der prioren Dichte

Approximation der Prioren Gaußdichte durch Samples

Verschiedene Verfahren mit unterschiedliche Komplexität, Effizienz, Genauigkeit

  • Zufälliges Sampling mit Zufallszahlengenerator →\rightarrow unabhängige Samples

  • Abtastung (z.B. äquidistantes Gitter)

  • Minimale Approximation auf den Hauptachsen

    • Verwendung von 2N2N oder 2N+12N + 1 samples (NN: #Dimension)

      wertkontinuierliche_nichtlineare_system-Minimal_Approximation.drawio

  • Genaue Approximation auf den Hauptachsen

    wertkontinuierliche_nichtlineare_system-Genau_Approximation.drawio

  • Allgemeine Sample-Approximation →\rightarrow Systematische Approximation durch Minimierung eines Gütemaßes

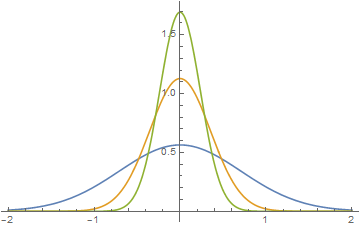
Einschub: Diracsche Deltafunktion

Betrachtung Grenzfall einer Gaußdichte

f(x,m,σ)=12πσexp⁡{−12(x−m)2σ2} f(x, m, \sigma)=\frac{1}{\sqrt{2 \pi} \sigma} \exp \left\{-\frac{1}{2} \frac{(x-m)^{2}}{\sigma^{2}}\right\}

für σ→0\sigma \rightarrow 0

Plotting verschiedener Gaußdichte für $m=0$.

Plotting verschiedener Gaußdichte für m=0m=0.

Dirasche Deltafunktion

δ(x−m)=lim⁡σ→0f(x,m,σ) \delta(x-m)=\lim _{\sigma \rightarrow 0} f(x, m, \sigma)

Wenn die Bereite gegen 0 (σ→0\sigma \to 0), die Höhe gegen unendlich.

∫−∞∞δ(x−m)dx=1 \int_{-\infty}^{\infty} \delta(x-m) d x=1

Definition: Diracsche Deltafunktion

$$ \delta(x)=\left\\{\begin{array}{cc} \text{Nicht definiert} & x=0 \\\\ 0 & \text { sonst } \end{array}\right. $$ $$ \int_{-\infty}^{\infty} \delta(x) d x=\int_{-\varepsilon}^{\varepsilon} \delta(x) d x=1, \varepsilon>0 $$
  • Laut Definition hat die Dirasche Deltafunktion alle Eigenschaften einer Dichte
  • Wichtige Eigenschaften
    • f(x)⋅δ(x−m)=f(m)δ(x−m)f(x) \cdot \delta(x-m)=f(m) \delta(x-m)
    • ∫Rf(x)δ(x−m)dx=f(m)\int_{\mathbb{R}} f(x) \delta(x-m) d x=f(m)

Heaviside Funktion (Unit Step Function)

Cumulative Verteilungsfunktion der Gaußdichte

F(x)=P(x≤x)=∫−∞xf(x)dx=12{1+erf⁡(x−m2σ)} F(x)=P(\boldsymbol{x} \leq x)=\int_{-\infty}^{x} f(x) d x=\frac{1}{2}\left\{1+\operatorname{erf}\left(\frac{x-m}{\sqrt{2} \sigma}\right)\right\}

Es gilt

f(x)=ddxF(x) f(x)=\frac{d}{d x} F(x)

Definition: Heaviside Funktion

$$ H(x-m)=\lim\_{\sigma \to 0} F(x)=\left\\{\begin{array}{ll} 1 & x>m \\\\ \frac{1}{2} & x=m \\\\ 0 & x

Cumulative Verteilungsfunktion von δ(x)\delta(x) ist H(x)H(x) mit

H(x)=∫−∞xδ(x)dxδ(x)=ddxH(x) \begin{array}{l} H(x)=\displaystyle\int_{-\infty}^{x} \delta(x) d x \\\\ \delta(x)=\frac{d}{d x} H(x) \end{array}

Multivariate Diracsche Deltafunktion

Dirasche Mischdichten (Dirac Mixture)

f(x)=∑i=1Lωiδ(x−xi) f(x)=\sum_{i=1}^{L} \omega_{i} \delta \left(x-x_{i}\right)

Multivariate Diracdichte

δ(x‾)=δ(x1)⋅δ(x2)⋅…,x‾=[x1,x2,…]⊤ \delta(\underline{x})=\delta\left(x_{1}\right) \cdot \delta\left(x_{2}\right) \cdot \ldots, \quad \underline{x}=\left[x_{1}, x_{2}, \ldots\right]^{\top}

Multivariate Dirasche Mischdichte

f(x‾)=∑i=1Lωiδ(x‾−x‾i) f(\underline{x})=\sum_{i=1}^{L} \omega_{i} \delta\left(\underline{x}-\underline{x}_{i}\right)

Umrechnung SNV →\rightarrow Allgemeine Gaußdichte

(SNV = Standard Normalverteilung N(0,1)\mathcal{N}(0, 1))

  • Natürliche Lösung für Problem
  • Verschiedene Möglichkeiten mit unterschiedlicher Komplexität und Effizienz

Angenommen: Wir haben ein Approximationsverfahren, das eine standardverteilung in merh-/höher-dimension approximieren kann.

  • Gegeben: Gaußdichte mit x^‾=0‾\underline{\hat{x}}=\underline{0} und Cx=IN\mathbf{C}_x = \mathbf{I}_N (NN-dim. Einheitsmatrix)
  • Gesucht: Dichte mit beliebigen Mittelwert y^‾\underline{\hat{y}} und Kovarianzmatrix Cy\mathbf{C}_y

Wir machen Cholesky-Zerlegung

Cy=Cy⋅Cy⊤ \mathbf{C}_{y}=\mathcal{C}_{y} \cdot \mathcal{C}_{y}^{\top}

wobei Cy\mathcal{C}_y eine untere Dreiecksmatrix.

Umrechnung

y‾=Cy⋅x‾+y^‾ \underline{y}=\mathcal{C}_{y} \cdot \underline{x}+\underline{\hat{y}}

Beweis:

E{y‾}=E{Cy⋅x‾+y^}=CyE{x‾}⏟=0‾+E{y^⏟=y‾}=y^‾ E\{\underline{y}\}=E\left\{\mathcal{C}_{y} \cdot \underline{x}+\hat{y}\right\}=\mathcal{C}_{y} \underbrace{E\{\underline{x}\}}_{=\underline{0}}+\underbrace{E\{\hat{y}}_{=\underline{y}}\}=\underline{\hat{y}} Cov⁡{y‾}=E{(y‾−E{y‾})(y‾−E{y‾)⊤}=E{(y‾−y^‾)(y‾−y^‾)⊤}=E{Cy⋅x‾⋅x‾⊤Cy⊤}=Cy⋅E{x‾x‾⊤}⏟=Cx=IN⋅Cy⊤=Cy⋅IN⋅Cy⊤=Cy⋅Cy⊤=Cy \begin{aligned} \operatorname{Cov}\{\underline{y}\} &=E\left\{(\underline{y}-E\{\underline{y}\})(\underline{y}-E\{\underline{y})^{\top}\right\} \\ &=E\left\{(\underline{y}-\underline{\hat{y}})(\underline{y}-\underline{\hat{y}})^{\top}\right\} \\ &=E\left\{\mathcal{C}_{y} \cdot \underline{x} \cdot \underline{x}^{\top} \mathcal{C}_{y}^{\top}\right\}\\ &=\mathcal{C}_{y} \cdot \underbrace{E\left\{\underline{x}\underline{x}^{\top}\right\}}_{=\mathbf{C}_{x}=\mathbf{I}_{N}} \cdot \mathcal{C}{y}^{\top} \\ &=\mathcal{C}_{y} \cdot \mathbf{I}_{N} \cdot \mathcal{C}_{y}^{\top}=\mathcal{C}_{y} \cdot \mathcal{C}_{y}^{\top} = \mathbf{C}_{y} \end{aligned}

Minimale Approximation SNV auf Hauptachsen

1D-Fall

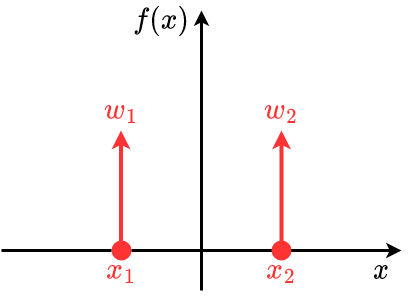
Die wahre Dichte f~(x)\tilde{f}(x) sei eine 1D Standardnormalverteilung (SNV). Die möchten wir darstellen über eine Dirac Mixture

wertkontinuierliche_nichtlineare_system-SNV_approx_1D.drawio f(x)=w1δ(x−x1)+w2δ(x−x2)w1,w2⩾0 f(x)=w_{1} \delta\left(x-x_{1}\right)+w_{2} \delta\left(x-x_{2}\right) \qquad w_{1}, w_{2} \geqslant 0

Gaußdichte ist symmetrisch ⇒\Rightarrow

w1=w2=w,x1=−x2 w_{1}=w_{2}=w, \quad x_{1}=-x_{2}

Integral soll gleich 1 sein.

∫Rf(x)dx=w1+w2=2w=!1⇒w=12 \int_{\mathbb{R}} f(x) d x=w_{1}+w_{2}=2 w \stackrel{!}{=} 1 \Rightarrow w=\frac{1}{2}

Erwartungswert:

Ef{x}=0=Ef~{x} E_{f}\{x\}=0=E_{\tilde{f}}\{x\}

Varianz:

Ef{x2}=∫Rx2f(x)dx=wx12+wx22=2wx12=!1⇒x12=1⇒x1=−1,x2=1 E_{f}\left\{x^{2}\right\}=\int_{\mathbb{R}} x^{2} f(x) d x=w x_{1}^{2}+w x_{2}^{2}=2 w x_{1}^{2} \stackrel{!}{=} 1 \Rightarrow x_{1}^{2}=1 \Rightarrow x_1 = -1, x_2 = 1

2D-Fall

wertkontinuierliche_nichtlineare_system-SNV_approx_2D.drawio f(x,y)=w1δ(x−x1)δ(y)+w2δ(x−x2)δ(y)w1,w2⩾0+v1δ(x)δ(y−y1)+v2δ(x)δ(y−y2)v1,v2⩾0 \begin{aligned} f(x, y)=& w_{1} \delta\left(x-x_{1}\right) \delta(y)+w_{2} \delta\left(x-x_{2}\right) \delta(y) & w_{1}, w_{2} \geqslant 0 \\ &+v_{1} \delta(x) \delta\left(y-y_{1}\right)+v_{2} \delta(x) \delta\left(y-y_{2}\right) & v_{1}, v_{2} \geqslant 0 \end{aligned}

Symmetrie ⇒\Rightarrow

w1=w2=v1=v2=w,x1=−x2,v1=−y2 w_{1}=w_{2}=v_{1}=v_{2}=w, \quad x_{1}=-x_{2}, \quad v_{1}=-y_{2}

Integral = 1

∫R2f(x,y)dxdy=w{∫Rs(x−x1)dx∫Rf(y)dy+…}=4w=!1⇒w=14 \int_{\mathbb{R}^{2}} f(x, y) d x d y=w\left\{\int_{\mathbb{R}} s\left(x-x_{1}\right) d x \int_{\mathbb{R}} f(y) d y+\ldots\right\}=4 w \stackrel{!}{=} 1 \Rightarrow w=\frac{1}{4}

Varianz

∬Rx2f(x,y)dxdy=wx12+wx22=2wx12=!1⇒x12=2⇒x1=−2,x2=2 \iint_{\mathbb{R}} x^{2} f(x, y) d x d y=w x_{1}^{2}+w x_{2}^{2}=2 w x_{1}^{2} \stackrel{!}{=} 1 \Rightarrow x_{1}^{2}=2 \Rightarrow x_1 = -\sqrt{2}, x_2 = \sqrt{2}

x,yx, y sind nicht unabhänging:

f(x,y)≠f(x)⋅f(y),E{x⋅y}=0 f(x, y) \neq f(x) \cdot f(y), E\{x \cdot y\}=0

N-dim Fall

w=12Nx‾=[x(1),x(2),…]⊤⇒x1(i)=−N,x2(i)=+N,i=1,…,N \begin{array}{c} w=\frac{1}{2 N} \quad \underline{x}=\left[x^{(1)}, x^{(2)}, \ldots\right]^{\top} \\ \Rightarrow \begin{equation} x_{1}^{(i)}=-\sqrt{N}, \quad x_{2}^{(i)}=+\sqrt{N}, \quad i=1, \ldots, N \end{equation} \end{array}

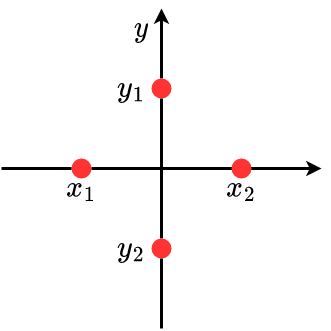
Ablauf des Filters mit Sampling der prioren Dichte

Messfunktion (Bsp.)

y=x3+v y = x^3 + v

Priore Schätzung: Gaußdichte f~p(x)=N(x,x^p,σp2)\tilde{f}_{p}(x)=\mathcal{N}\left(x, \hat{x}_{p}, \sigma_{p}^{2}\right)

Rauschen: v∼f~v(v)=N(v,0,σv2)v \sim \tilde{f}_v(v) = \mathcal{N}(v, 0, \sigma_v^2)

截屏2022-09-12 22.29.08

Approximation

fp(x)=12δ(x−x1)+12δ(x−x2) f_{p}(x)=\frac{1}{2} \delta\left(x-x_{1}\right)+\frac{1}{2} \delta\left(x-x_{2}\right)

wobei

x1=x^p−σpx2=x^p+σp x_1 = \hat{x}_p - \sigma_p \quad x_2 = \hat{x}_p + \sigma_p fv(v)=12δ(x−σv⏟=v1)+12δ(x+σv⏟=v2) f_v(v)=\frac{1}{2} \delta(\underbrace{x - \sigma_{v}}_{=v_{1}})+\frac{1}{2} \delta(\underbrace{x+\sigma_{v}}_{=v_{2}})

Dann

yij=xi3+vji=1,2,j=1,2 y_{i j}=x_{i}^{3}+v_{j} \qquad i=1,2 , j=1,2

Wir sampeln für xx und vv jeweils 2 Samples. Dann kriegen wir 4 Paare (x,y)(x, y): (x1,y11),(x1,y12),(x2,y21),(x2,y22)(x_1, y_{11}), (x_1, y_{12}), (x_2, y_{21}), (x_2, y_{22}), also die 4 violette Punkte im Bild.

Wir nehmen an, dass x,yx, y gemeinsam Gaußverteilt sind. Dann berechnen wir mit dieser 4 Punkte den Mittelwert und Kovarianz, und fitten wir eine Gaußdichte (Moment matching).

Wir haben auch die Messung y^\hat{y}, die diese approximierte Gaußdichte schneidet. Mit y^\hat{y} können wir jetzt den probabilistischen Kalman Filter durchführen.