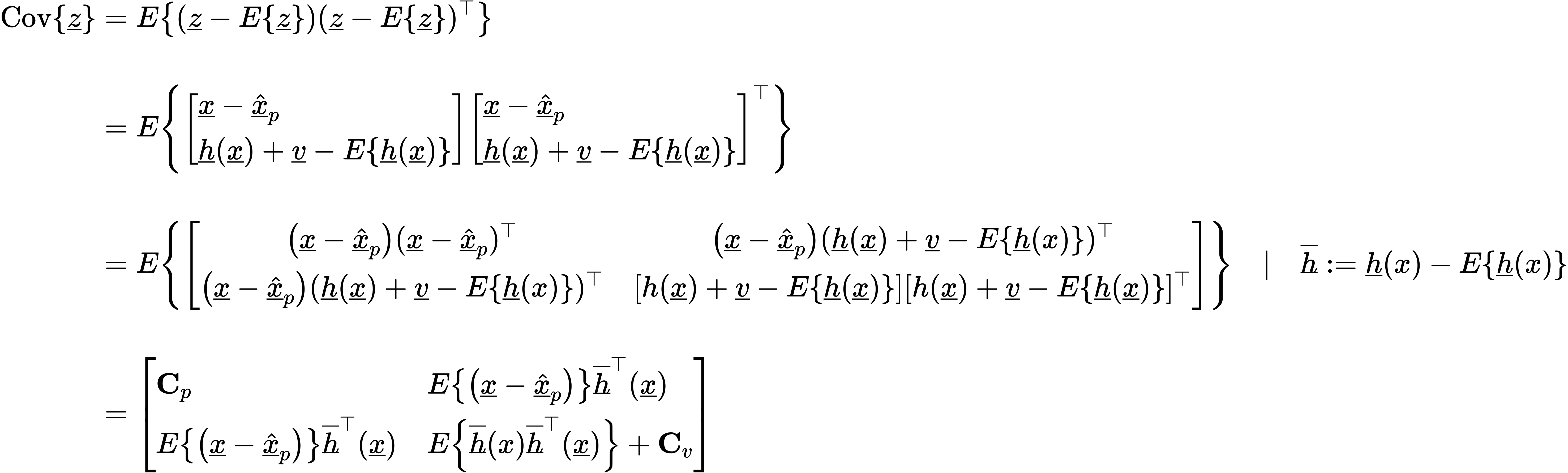Nichtlineare Schätzung Approximation durch Linearisierung Idea
Linearisierung der nichtlinear Funktion
(Normal/Linear) Kalman Filter anwenden
Systemmodell x ‾ k + 1 = a ‾ k ( x ‾ k , u ‾ k ) (Systemmodell)
\underline{x}_{k+1}=\underline{a}_{k}\left(\underline{x}_{k}, \underline{u}_{k}\right)
\tag{Systemmodell}
x k + 1 = a k ( x k , u k ) ( Systemmodell ) Linearisierung der rechten Seite von (Systemmodell) \text{(Systemmodell)} (Systemmodell) x ‾ ‾ k , u ‾ ‾ k \underline{\overline{x}}_k, \underline{\overline{u}}_k x k , u k
a ‾ k ( x ‾ k , u ‾ k ) = a ‾ k ( x ‾ ‾ k , u ‾ ‾ k ) + ∂ a ‾ k ( x ‾ k , u ‾ k ) ∂ x ‾ k ⊤ ∣ x ‾ k = x ˉ ‾ k , u ‾ k = u ˉ ‾ k ⏞ = A ⋅ ( x ‾ k − x ‾ ‾ k ) ⏞ = Δ x ‾ k + THO + ∂ a ‾ k ( x ‾ k , u ‾ k ) ∂ u ‾ k ⊤ ∣ x ‾ k = x ˉ ‾ k , u ‾ k = u ˉ ‾ ‾ k ⏟ = B ⋅ ( u ‾ k − u ‾ ‾ k ) + THO
\begin{array}{ll}
&\underline{a}_{k}\left(\underline{x}_{k}, \underline{u}_{k}\right) = \underline{a}_{k}\left(\underline{\overline{x}}_k, \underline{\overline{u}}_k\right) &+ \overbrace{\left.\frac{\partial \underline{a}_{k}\left(\underline{x}_{k}, \underline{u}_{k}\right)}{\partial \underline{x}_{k}^{\top}}\right|_{\underline{x}_{k}=\underline{\bar{x}}_{k}, \underline{u}_{k}=\underline{\bar{u}}_{k}}}^{=\mathbf{A}} \cdot \overbrace{(\underline{x}_{k} - \underline{\overline{x}}_k)}^{=\Delta \underline{x}_{k}} + \text{THO} \\\\
& & + \underbrace{\left.\frac{\partial \underline{a}_{k}\left(\underline{x}_{k}, \underline{u}_{k}\right)}{\partial \underline{u}_{k}^{\top}}\right|_{\underline{x}_{k}=\underline{\bar{x}}_{k}, \underline{u}_{k}=\overline{\underline{\bar{u}}}_{k}}}_{=\mathbf{B}} \cdot (\underline{u}_{k} - \underline{\overline{u}}_k) + \text{THO}
\end{array}
a k ( x k , u k ) = a k ( x k , u k ) + ∂ x k ⊤ ∂ a k ( x k , u k ) x k = x ˉ k , u k = u ˉ k = A ⋅ ( x k − x k ) = Δ x k + THO + = B ∂ u k ⊤ ∂ a k ( x k , u k ) x k = x ˉ k , u k = u ˉ k ⋅ ( u k − u k ) + THO Annahme
Ableitung existiert a ‾ k ( ⋅ , ⋅ ) \underline{a}_k(\cdot, \cdot) a k ( ⋅ , ⋅ ) x ‾ ‾ k , u ‾ ‾ k \underline{\overline{x}}_k, \underline{\overline{u}}_k x k , u k Vernachlässigen von THO ⇒ \text{THO} \Rightarrow THO ⇒
a ‾ k ( x ‾ k , u ‾ k ) ≈ a ‾ k ( x ‾ ‾ k , u ‾ ‾ k ) + A k ( x ‾ k − x ‾ ‾ k ) + B k ( u ‾ k − u ‾ ‾ k )
\underline{a}_{k}\left(\underline{x}_{k}, \underline{u}_{k}\right) \approx \underline{a}_{k}\left(\underline{\overline{x}}_k, \underline{\overline{u}}_k\right)+\mathbf{A}_{k}\left(\underline{x}_k-\underline{\overline{x}}_k\right)+\mathbf{B}_{k}\left(\underline{u}_{k}-\underline{\overline{u}}_k\right)
a k ( x k , u k ) ≈ a k ( x k , u k ) + A k ( x k − x k ) + B k ( u k − u k ) Für die linke Seite von ( Systemmodell ) (\text{Systemmodell}) ( Systemmodell )
x ‾ k + 1 = x ‾ ‾ k + 1 + Δ x ‾ k + 1
\underline{x}_{k+1}= \underline{\overline{x}}_{k+1} + \Delta \underline{x}_{k+1}
x k + 1 = x k + 1 + Δ x k + 1 Für u ‾ k \underline{u}_{k} u k
u ‾ k : = u ^ ‾ k + w ‾ k
\underline{u}_{k}:=\underline{\hat{u}}_{k}+\underline{w}_{k}
u k := u ^ k + w k mit E { w ‾ k } = 0 , Cov { w ‾ k } = C k w E\left\{\underline{w}_{k}\right\}=0, \operatorname{Cov}\left\{\underline{w}_{k}\right\}=\mathbf{C}_{k}^{w} E { w k } = 0 , Cov { w k } = C k w
Durch obige Linearisierung der beiden Seiten kann man das Systemmodell so schreiben:
x ‾ ‾ k + 1 + Δ x ‾ k + 1 ≈ a ‾ k ( x ‾ ‾ k , u ‾ ‾ k ) + A k Δ x ‾ k + w ‾ k ′
\underline{\overline{x}}_{k+1} + \Delta \underline{x}_{k+1} \approx \underline{a}_{k}\left(\underline{\overline{x}}_k, \underline{\overline{u}}_k\right)+\mathbf{A}_{k}\Delta \underline{x}_k+\underline{w}_k^\prime
x k + 1 + Δ x k + 1 ≈ a k ( x k , u k ) + A k Δ x k + w k ′ Nominalteil
x ‾ ‾ k + 1 = a ‾ k ( x ‾ ‾ k , u ‾ ‾ k )
\underline{\overline{x}}_{k+1} = \underline{a}_{k}\left(\underline{\overline{x}}_k, \underline{\overline{u}}_k\right)
x k + 1 = a k ( x k , u k ) Differentialteil
Δ x ‾ k + 1 ≈ A k Δ x ‾ k + w ‾ k ′
\Delta \underline{x}_{k+1} \approx \mathbf{A}_{k}\Delta \underline{x}_k+\underline{w}_k^\prime
Δ x k + 1 ≈ A k Δ x k + w k ′ Messgleichung y ‾ k = h ‾ k ( x ‾ k , v ‾ k ) (Messgleichung)
\underline{y}_{k}=\underline{h}_{k}\left(\underline{x}_{k}, \underline{v}_{k}\right)
\tag{Messgleichung}
y k = h k ( x k , v k ) ( Messgleichung ) Linearisierung der rechten Seite um x ˉ ‾ k , v ˉ ‾ k \underline{\bar{x}}_{k}, \underline{\bar{v}}_{k} x ˉ k , v ˉ k
h ‾ k ( x ‾ k , v ‾ k ) ≈ h ‾ k ( x ˉ ‾ k , v ˉ ‾ k ) + H k ⋅ ( x ‾ k − x ˉ ‾ k ) ⏟ = Δ x ‾ k + L k ⋅ ( v ‾ k − v ˉ ‾ k )
\underline{h}_{k}\left(\underline{x}_{k}, \underline{v}_{k}\right) \approx \underline{h}_{k}\left(\underline{\bar{x}}_{k}, \underline{\bar{v}}_{k}\right)+\mathbf{H}_{k} \cdot \underbrace{\left(\underline{x}_{k}-\underline{\bar{x}}_{k}\right)}_{=\Delta \underline{x}_k}+\mathbf{L}_{k} \cdot\left(\underline{v}_{k}-\underline{\bar{v}}_{k}\right)
h k ( x k , v k ) ≈ h k ( x ˉ k , v ˉ k ) + H k ⋅ = Δ x k ( x k − x ˉ k ) + L k ⋅ ( v k − v ˉ k ) mit Jacobi-Matrizen
H k = ∂ h ‾ k ( x ‾ k , v ‾ k ) ∂ x ‾ k ⊤ ∣ x ‾ k = x ‾ k , v ‾ k = v ˉ ‾ k L k = ∂ h ‾ k ( x ‾ k , v ‾ k ) ∂ v ‾ k ⊤ ∣ x ‾ k = x ‾ k , v ‾ k = v ˉ ‾ k
\mathbf{H}_{k}=\left.\frac{\partial \underline{h}_{k}\left(\underline{x}_{k}, \underline{v}_{k}\right)}{\partial \underline{x}_{k}^{\top}}\right|_{\underline{x}_{k}=\underline{x}_{k}, \underline{v}_{k}=\underline{\bar{v}}_{k}} \qquad
\mathbf{L}_{k}=\left.\frac{\partial \underline{h}_{k}\left(\underline{x}_{k}, \underline{v}_{k}\right)}{\partial \underline{v}_{k}^{\top}}\right|_{\underline{x}_{k}=\underline{x}_{k}, \underline{v}_{k}=\underline{\bar{v}}_{k}}
H k = ∂ x k ⊤ ∂ h k ( x k , v k ) x k = x k , v k = v ˉ k L k = ∂ v k ⊤ ∂ h k ( x k , v k ) x k = x k , v k = v ˉ k Sei v ˉ ‾ k = v ^ ‾ k \underline{\bar{v}}_{k} = \underline{\hat{v}}_{k} v ˉ k = v ^ k mittelwertfreies v ‾ k ⇒ v ^ ‾ k = 0 ‾ \underline{v}_{k} \Rightarrow \underline{\hat{v}}_{k} = \underline{0} v k ⇒ v ^ k = 0
Das Effektive Rauschen ist dann
v ‾ k ′ = L k ⋅ v ‾ k
\underline{v}_{k}^\prime = \mathbf{L}_{k} \cdot \underline{v}_{k}
v k ′ = L k ⋅ v k mit
E { v ‾ k ′ } = 0 ‾ , Cov { v ‾ k ′ } = L k ⋅ C k v ⋅ L k ⊤
E\left\{\underline{v}_{k}^{\prime}\right\}=\underline{0}, \quad \operatorname{Cov}\left\{\underline{v}_{k}^{\prime}\right\}=\mathbf{L}_{k} \cdot \mathbf{C}_{k}^{v} \cdot \mathbf{L}_{k}^{\top}
E { v k ′ } = 0 , Cov { v k ′ } = L k ⋅ C k v ⋅ L k ⊤ Damit kann man die Messgliechung so umschreiben:
y ‾ k = y ˉ ‾ k + Δ y ‾ k ≈ h ‾ k ( x ˉ ‾ k , v ˉ ‾ k ) + H k Δ x ‾ k + v ‾ k ′
\underline{y}_{k}=\underline{\bar{y}}_{k}+\Delta \underline{y}_{k} \approx \underline{h}_{k}\left(\underline{\bar{x}}_{k}, \underline{\bar{v}}_{k}\right)+\mathbf{H}_{k} \Delta \underline{x}_{k}+\underline{v}_{k}^{\prime}
y k = y ˉ k + Δ y k ≈ h k ( x ˉ k , v ˉ k ) + H k Δ x k + v k ′ Nominalteil
y ˉ ‾ k = h ‾ k ( x ˉ ‾ k , v ˉ ‾ k )
\underline{\bar{y}}_{k} = \underline{h}_{k}\left(\underline{\bar{x}}_{k}, \underline{\bar{v}}_{k}\right)
y ˉ k = h k ( x ˉ k , v ˉ k ) Differentialteil
Δ y ‾ k ≈ H k Δ x ‾ k + v ‾ k ′
\Delta \underline{y}_{k} \approx \mathbf{H}_{k} \Delta \underline{x}_{k}+\underline{v}_{k}^{\prime}
Δ y k ≈ H k Δ x k + v k ′ Erweitertes Kalmanfilter (EKF) 💡Linearisierung um jeweils beste Schätzung
Prädiktion
Filterung
Berechnung von y ˉ ‾ k \underline{\bar{y}}_k y ˉ k
y ˉ ‾ k = h ‾ k ( x ˉ ‾ k p , v ^ ‾ k )
\underline{\bar{y}}_k = \underline{h}_k(\underline{\bar{x}}_k^p, \underline{\hat{v}}_k)
y ˉ k = h k ( x ˉ k p , v ^ k ) Berechnung von Δ y ‾ k \Delta \underline{y}_k Δ y k
Δ y ‾ k = y ^ ‾ k − y ˉ ‾ k
\Delta \underline{y}_{k}=\underline{\hat{y}}_{k}-\underline{\bar{y}}_{k}
Δ y k = y ^ k − y ˉ k y ^ ‾ k \underline{\hat{y}}_{k} y ^ k und
Δ y ‾ k ≈ H k ⋅ ( x ‾ k e − x ^ ‾ k p ) + v ‾ k ′
\Delta \underline{y}_{k} \approx \mathbf{H}_{k} \cdot\left(\underline{x}_{k}^{e}-\underline{\hat{x}}_{k}^{p}\right)+\underline{v}_{k}^{\prime}
Δ y k ≈ H k ⋅ ( x k e − x ^ k p ) + v k ′ mit
H k = ∂ h ‾ k ( x ‾ k , v ‾ k ) ∂ x ‾ k ⊤ ∣ x ‾ k = x ^ ‾ k p , v ‾ k = v ^ ‾ k L k = ∂ h ‾ k ( x ‾ k , v ‾ k ) ∂ v ‾ k ⊤ ∣ x ‾ k = x ^ ‾ k p , v ‾ k = v ^ ‾ k
\mathbf{H}_{k}=\left.\frac{\partial \underline{h}_{k}\left(\underline{x}_{k}, \underline{v}_{k}\right)}{\partial \underline{x}_{k}^{\top}}\right|_{\underline{x}_{k}=\underline{\hat{x}}_{k}^{p}, \underline{v}_{k}=\underline{\hat{v}}_{k}} \qquad
\mathbf{L}_{k}=\left.\frac{\partial \underline{h}_{k}\left(\underline{x}_{k}, \underline{v}_{k}\right)}{\partial \underline{v}_{k}^{\top}}\right|_{\underline{x}_{k}=\underline{\hat{x}}_{k}^{p}, \underline{v}_{k}=\underline{\hat{v}}_{k}}
H k = ∂ x k ⊤ ∂ h k ( x k , v k ) x k = x ^ k p , v k = v ^ k L k = ∂ v k ⊤ ∂ h k ( x k , v k ) x k = x ^ k p , v k = v ^ k Filterung Schritt
K k = C k p H k ⊤ ( L k C k v L k ⊤ + H k C k p H k T ) − 1 x ‾ ^ k e = x ‾ ^ k p + K k [ y ‾ ^ k − h ‾ k ( x ‾ ^ k p , v ‾ ^ k ) ] C k e = C k p − K k H k C k p = ( I − K k H k ) C k p
\begin{aligned}
\mathbf{K}_{k}&=\mathbf{C}_{k}^{p} \mathbf{H}_{k}^{\top}\left(\mathbf{L}_{k} \mathbf{C}_{k}^{v} \mathbf{L}_{k}^{\top}+\mathbf{H}_{k} \mathbf{C}_{k}^{p} \mathbf{H}_{k}^{T}\right)^{-1} \\\\
\hat{\underline{x}}_{k}^{e}&=\hat{\underline{x}}_{k}^{p}+\mathbf{K}_{k}\left[\hat{\underline{y}}_{k}-\underline{h}_{k}\left(\hat{\underline{x}}_{k}^{p}, \hat{\underline{v}}_{k}\right)\right] \\\\
\mathbf{C}_{k}^{e}&=\mathbf{C}_{k}^{p}-\mathbf{K}_{k} \mathbf{H}_{k} \mathbf{C}_{k}^{p} = (\mathbf{I} - \mathbf{K}_{k} \mathbf{H}_{k})\mathbf{C}_{k}^{p}
\end{aligned}
K k x ^ k e C k e = C k p H k ⊤ ( L k C k v L k ⊤ + H k C k p H k T ) − 1 = x ^ k p + K k [ y ^ k − h k ( x ^ k p , v ^ k ) ] = C k p − K k H k C k p = ( I − K k H k ) C k p Probleme bei Linearisierung Berechnung der posteriore Verteilung nur gut für “schwache” Nichtlinearität
→ \rightarrow →
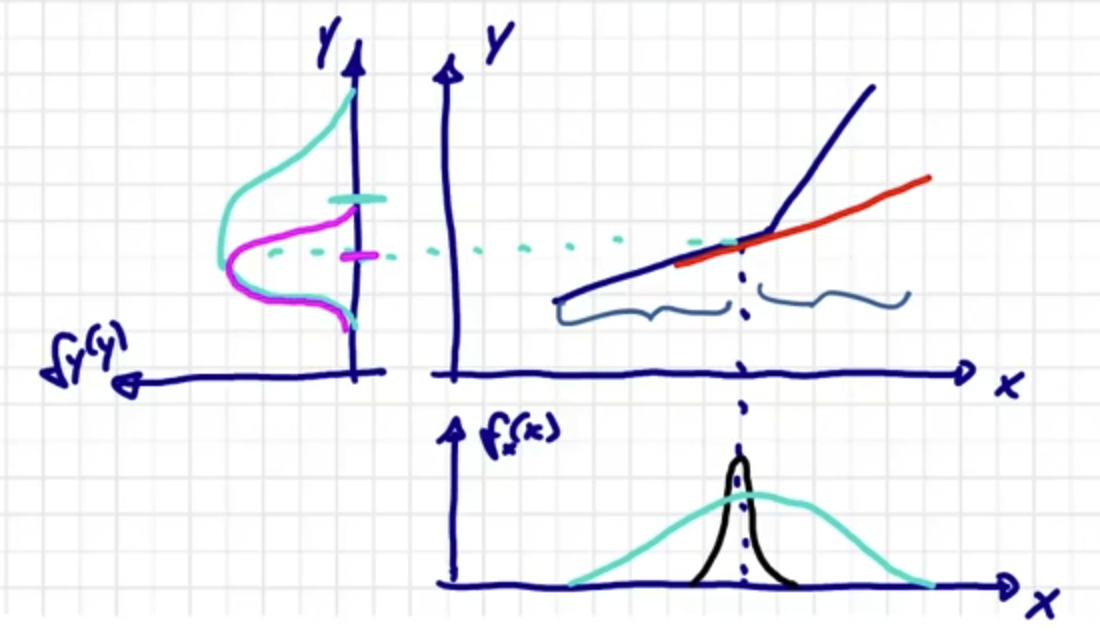
Wenn wir für priore Dichte kleines/schmales Rauschen (unten, schwarz) verwenden, dann funktioniert es gut.
Wenn wir das Rauschen breiter machen (unten, grün), dann kommt ein Problem vor, dass die resultierende Dichte von y y y
Induzierte nichtlinearität heißt: wir können gar nicht sagen, die ist absolut betrachtet, besonders linear oder besonders nichtlinear. Es ist potential, Problem zu machen. Aber sie macht kein Problem, solange ich mich nur in den linken Bereich oder nur in den rechten Bereich des “Knickpunkt” aufhalten. Wenn wir die Dichte habe, die über den “Knickpunkt” weggeht, dann bekomme ich Problem. Das ist die induzierte nichtlinearität, die durch das Rauschen induziert wird.
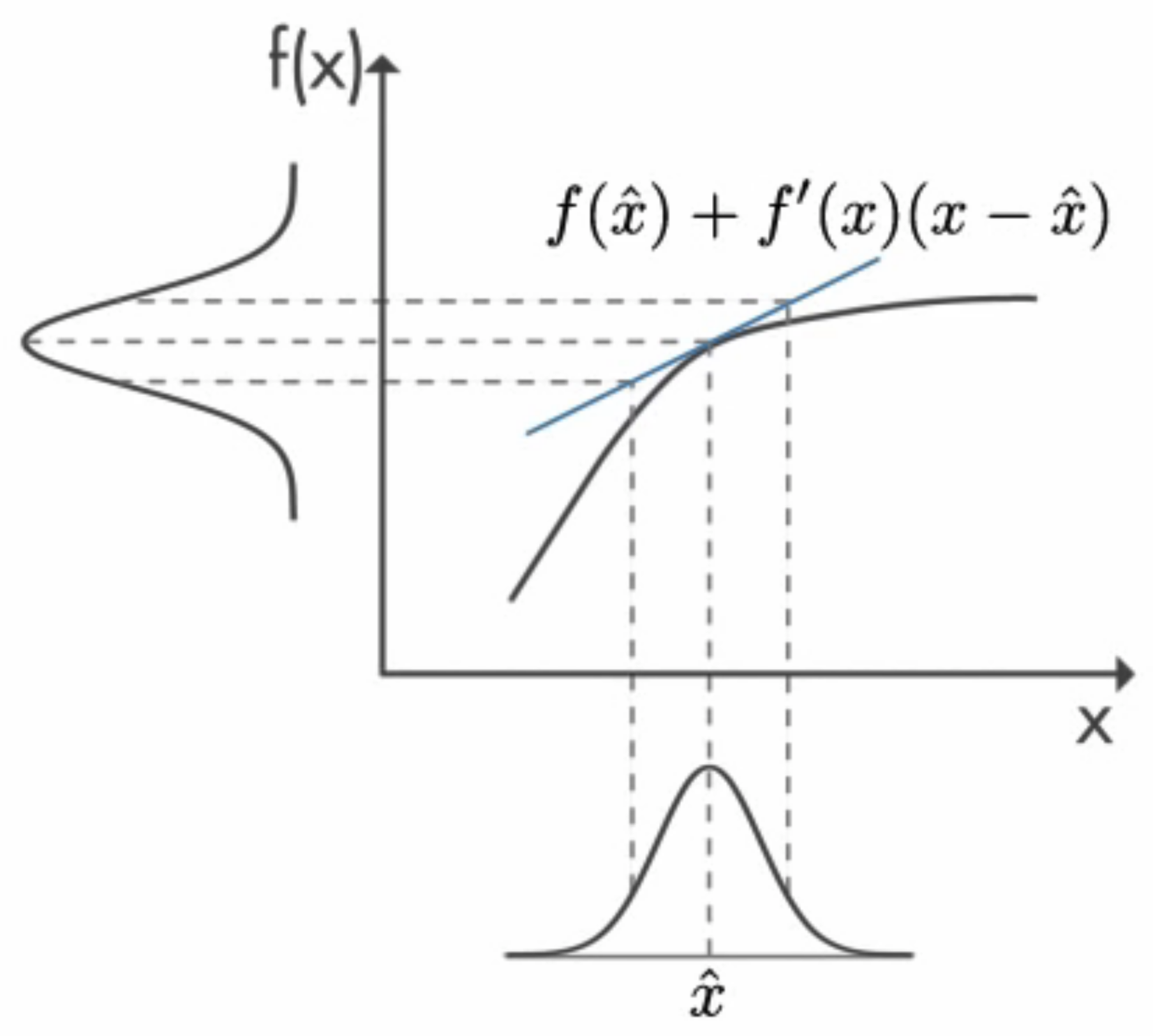
Linearisierung nur um einen Punkt
Linearisiertes System ist i.A. zeitvariant, auch wenn originalsytstem zeitinvariant ist, da Linearisierung vom Schätzwert abhängt.
Erwartungswertbildung Gegeben:
Funktion y ‾ = g ‾ ( x ‾ ) \underline{y}=\underline{g}(\underline{x}) y = g ( x ) x ‾ ∼ f x ( x ) \underline{x} \sim f_x(x) x ∼ f x ( x ) Gesucht: Bestimmte Momente von y ‾ \underline{y} y
Z.B. für skalares Fall
y = g ( x )
y = g(x)
y = g ( x ) suchen wir E { y j } , j ∈ N E\left\{y^{j}\right\}, j \in \mathbb{N} E { y j } , j ∈ N
Wir wissen
E { y i } = ∫ R y j f y ( y ) d y
E\left\{y^{i}\right\}=\int_{\mathbb{R}} y^{j} f_{y}(y) d y
E { y i } = ∫ R y j f y ( y ) d y Aber
f y ( y ) f_y(y) f y ( y ) Falls berechbar, die Berechnung von f y ( y ) f_y(y) f y ( y ) Theorem (Dualität bei Erwartungswertbildung)
E\_{f\_y}\left\\{y^{j}\right\\}=E\_{f\_{x}}\left\\{[g(x)]^{j}\right\\}=\int\_{\mathbb{R}}[g(x)]^{j} f\_{x}(x) d x
f y ( y ) f_y(y) f y ( y ) Nützlich, wennf y ( y ) f_y(y) f y ( y ) 1-order nichtlineare Momente von f x ( ⋅ ) f_x(\cdot) f x ( ⋅ ) Für sample-basierte Approximation der prioren Dichte f x ( x ) f_x(x) f x ( x )
f x ( x ) = ∑ i = 1 L w i δ ( x − x i )
f_{x}(x)=\sum_{i=1}^{L} w_{i} \delta\left(x-x_{i}\right)
f x ( x ) = i = 1 ∑ L w i δ ( x − x i ) ist berechnung der posterioren Dichte f y ( y ) f_y(y) f y ( y )
f y ( y ) = ∑ i = 1 L w i δ ( y − y i ) , y i = g ( x i )
f_y(y)=\sum_{i=1}^{L} w_{i} \delta\left(y-y_{i}\right), \quad y_{i}=g\left(x_{i}\right)
f y ( y ) = i = 1 ∑ L w i δ ( y − y i ) , y i = g ( x i ) Damit
E { y j } = ∫ R y j f y ( y ) d y = ∑ i = 1 L w i y i j = ∑ i = 1 L w i [ g ( x i ) ] j
E\left\{y^{j}\right\}=\int_{\mathbb{R}} y^{j} f_{y}(y) d y=\sum_{i=1}^{L} w_{i} y_{i}^{j}=\sum_{i=1}^{L} w_{i}\left[g\left(x_{i}\right)\right]^{j}
E { y j } = ∫ R y j f y ( y ) d y = i = 1 ∑ L w i y i j = i = 1 ∑ L w i [ g ( x i ) ] j und
E { [ g ( x ) ] j } = ∫ R [ g ( x ) ] j f x ( x ) d x = ∑ i = 1 L w i [ g ( x i ) ] j
E\left\{[g(x)]^{j}\right\}=\int_{\mathbb{R}}[g(x)]^{j} f_{x}(x) d x=\sum_{i=1}^{L} w_{i}\left[g\left(x_{i}\right)\right]^{j}
E { [ g ( x ) ] j } = ∫ R [ g ( x ) ] j f x ( x ) d x = i = 1 ∑ L w i [ g ( x i ) ] j Die Berechnungen sind in diesem Fall identisch, aber im allgemeinem Fall gilt dies NICHT! 🤪
Systemmodell
x k + 1 = a ‾ k ( x ‾ k , u ‾ k )
x_{k+1}=\underline{a}_{k}\left(\underline{x}_{k}, \underline{u}_{k}\right)
x k + 1 = a k ( x k , u k ) x ‾ \underline{x} x u ‾ \underline{u} u Für einen Kalman Filter, wir möchte in nächsten Schritt die Erwartungswert und die Kovarianzmatrix haben.
Erwartungswert
x ^ k + 1 p = E { a ‾ k ( x ‾ k , u ‾ k ) } = ∫ R N ∫ R p a ‾ k ( x ‾ k , u ‾ k ) f k x u ( x ‾ k , u ‾ k ) d x ‾ k d u ‾ k
\hat{x}_{k+1}^{p}=E\left\{\underline{a}_{k}\left(\underline{x}_{k}, \underline{u}_{k}\right)\right\}=\int_{\mathbb{R}^{N}} \int_{\mathbb{R}^{p}} \underline{a}_{k}\left(\underline{x}_{k}, \underline{u}_{k}\right) f_{k}^{x u}\left(\underline{x}_{k}, \underline{u}_{k}\right) d\underline{x}_{k} d\underline{u}_{k}
x ^ k + 1 p = E { a k ( x k , u k ) } = ∫ R N ∫ R p a k ( x k , u k ) f k xu ( x k , u k ) d x k d u k In der Regel sind x ‾ k , u ‾ k \underline{x}_{k}, \underline{u}_{k} x k , u k
f k x u ( x ‾ k , u ‾ k ) = f k e ( x ‾ k ) ⋅ f k u ( u ‾ k ) .
f_{k}^{x u}\left(\underline{x}_{k}, \underline{u}_{k}\right) = f_{k}^{e}\left(\underline{x}_{k}\right) \cdot f_{k}^{u}\left(\underline{u}_{k}\right).
f k xu ( x k , u k ) = f k e ( x k ) ⋅ f k u ( u k ) . Und nehme an, dass x ‾ k , u ‾ k \underline{x}_{k}, \underline{u}_{k} x k , u k
f k e ( x ‾ u ) = N ( x ‾ k , x ^ k e , C k e ) f k u ( u ‾ k ) = N ( u ‾ k , u ‾ ^ k , C k w )
\begin{aligned}
f_{k}^{e}\left(\underline{x}_{u}\right) &= \mathcal{N}(\underline{x}_{k}, \hat{x}_{k}^{e}, \mathbf{C}_{k}^{e}) \\\\
f_{k}^{u}\left(\underline{u}_{k}\right) &= \mathcal{N}\left(\underline{u}_{k}, \hat{\underline{u}}_{k}, \mathbf{C}_{k}^{w}\right)
\end{aligned}
f k e ( x u ) f k u ( u k ) = N ( x k , x ^ k e , C k e ) = N ( u k , u ^ k , C k w ) Für additives Rauschen
x ‾ k + 1 = a ‾ k ( x ‾ k ) + u ‾ k ( = a ‾ k ( x ‾ k ) + ( u ^ ‾ k + w ‾ k ) )
\underline{x}_{k+1}=\underline{a}_{k}\left(\underline{x}_{k}\right)+\underline{u}_{k} \left(= \underline{a}_{k}\left(\underline{x}_{k}\right)+(\underline{\hat{u}}_{k} + \underline{w}_k)\right)
x k + 1 = a k ( x k ) + u k ( = a k ( x k ) + ( u ^ k + w k ) ) gilt
x ^ ‾ k + 1 p = ∫ R n a ‾ k ( x ‾ k ) ⋅ f k e ( x ‾ k ) d x ‾ k + u ^ ‾ k
\underline{\hat{x}}_{k+1}^{p}=\int_{\mathbb{R}^{n}} \underline{a}_{k}\left(\underline{x}_{k}\right) \cdot f_{k}^{e}\left(\underline{x}_{k}\right) d \underline{x}_{k}+\underline{\hat{u}}_{k}
x ^ k + 1 p = ∫ R n a k ( x k ) ⋅ f k e ( x k ) d x k + u ^ k Dann ist
x ‾ k + 1 − x ^ ‾ k + 1 p = ( a ‾ k ( x ‾ k ) + ( u ^ ‾ k + w ‾ k ) ) − ( ∫ R n a ‾ k ( x ‾ k ) ⋅ f k e ( x ‾ k ) d x ‾ k + u ^ ‾ k ) = a ‾ k ( x ‾ k ) − ∫ R n a ‾ k ( x ‾ k ) ⋅ f k e ( x ‾ k ) d x ‾ k ⏟ : = a ˉ ‾ k ( x ‾ k ) + w ‾ k
\begin{aligned}
\underline{x}_{k+1} - \underline{\hat{x}}_{k+1}^{p} &= (\underline{a}_{k}(\underline{x}_{k})+(\underline{\hat{u}}_{k} + \underline{w}_k)) - \left(\int_{\mathbb{R}^{n}} \underline{a}_{k}\left(\underline{x}_{k}\right) \cdot f_{k}^{e}\left(\underline{x}_{k}\right) d \underline{x}_{k}+\underline{\hat{u}}_{k}\right) \\\\
&= \underbrace{\underline{a}_{k}(\underline{x}_{k}) - \int_{\mathbb{R}^{n}} \underline{a}_{k}\left(\underline{x}_{k}\right) \cdot f_{k}^{e}\left(\underline{x}_{k}\right) d \underline{x}_{k}}_{:= \underline{\bar{a}}_{k}(\underline{x}_{k})} + \underline{w}_k
\end{aligned}
x k + 1 − x ^ k + 1 p = ( a k ( x k ) + ( u ^ k + w k )) − ( ∫ R n a k ( x k ) ⋅ f k e ( x k ) d x k + u ^ k ) = := a ˉ k ( x k ) a k ( x k ) − ∫ R n a k ( x k ) ⋅ f k e ( x k ) d x k + w k Die Kovarianzmatrix ist
C k + 1 p = E { ( x ‾ k + 1 − x ^ ‾ k + 1 p ) ( x ‾ k + 1 − x ^ ‾ k + 1 p ) ⊤ } = E { ( a ˉ ‾ k ( x ‾ k ) + w ‾ k ) ( a ˉ ‾ k ( x ‾ k ) + w ‾ k ) ⊤ } = E { a ˉ ‾ k ( x ‾ k ) a ˉ ‾ k ⊤ ( x ‾ k ) + w ‾ k a ˉ ‾ k ( x ‾ k ) + a ˉ ‾ k ( x ‾ k ) w ‾ k ⊤ + w ‾ k w ‾ k ⊤ } = E { a ˉ ‾ k ( x ‾ k ) a ˉ ‾ k ⊤ ( x ‾ k ) } + E { w ‾ k a ˉ ‾ k ( x ‾ k ) } ⏟ = 0 + E { a ˉ ‾ k ( x ‾ k ) w ‾ k ⊤ } ⏟ = 0 + E { w ‾ k w ‾ k ⊤ } = E { a ˉ ‾ k ( x ‾ k ) a ˉ ‾ k ⊤ ( x ‾ k ) } + E { w ‾ k w ‾ k ⊤ } = ∫ R N a ‾ ‾ k ( x ‾ k ) a ‾ ‾ k ⊤ ( x k ) f k e ( x ‾ k ) d x ‾ k + C k w
\begin{aligned}
\mathbf{C}_{k+1}^{p} &= E\left\{\left(\underline{x}_{k+1}-\underline{\hat{x}}_{k+1}^{p}\right)(\underline{x}_{k+1}-\underline{\hat{x}}_{k+1}^{p})^{\top}\right\} \\\\
&= E\left\{(\underline{\bar{a}}_{k}(\underline{x}_{k}) + \underline{w}_k) (\underline{\bar{a}}_{k}(\underline{x}_{k}) + \underline{w}_k) ^ \top\right\} \\\\
&= E\left\{\underline{\bar{a}}_{k}(\underline{x}_k) \underline{\bar{a}}_{k}^\top(\underline{x}_k) + \underline{w}_k\underline{\bar{a}}_{k}(\underline{x}_k) + \underline{\bar{a}}_{k}(\underline{x}_k)\underline{w}_k^\top + \underline{w}_k\underline{w}_k^\top\right\} \\\\
&= E\left\{\underline{\bar{a}}_{k}(\underline{x}_k) \underline{\bar{a}}_{k}^\top(\underline{x}_k)\right\} + \underbrace{E\left\{\underline{w}_k\underline{\bar{a}}_{k}(\underline{x}_k)\right\}}_{=0} + \underbrace{E\left\{\underline{\bar{a}}_{k}(\underline{x}_k)\underline{w}_k^\top\right\}}_{=0} + E\left\{\underline{w}_k\underline{w}_k^\top\right\} \\\\
&= E\left\{\underline{\bar{a}}_{k}(\underline{x}_k) \underline{\bar{a}}_{k}^\top(\underline{x}_k)\right\} + E\left\{\underline{w}_k\underline{w}_k^\top\right\} \\\\
&= \int_{\mathbb{R}^{N}} \overline{\underline{a}}_{k}\left(\underline{x}_{k}\right) \overline{\underline{a}}_{k}^{\top}\left(x_{k}\right) f_{k}^{e}\left(\underline{x}_{k}\right) d \underline{x}_{k}+\mathbf{C}_{k}^{w}
\end{aligned}
C k + 1 p = E { ( x k + 1 − x ^ k + 1 p ) ( x k + 1 − x ^ k + 1 p ) ⊤ } = E { ( a ˉ k ( x k ) + w k ) ( a ˉ k ( x k ) + w k ) ⊤ } = E { a ˉ k ( x k ) a ˉ k ⊤ ( x k ) + w k a ˉ k ( x k ) + a ˉ k ( x k ) w k ⊤ + w k w k ⊤ } = E { a ˉ k ( x k ) a ˉ k ⊤ ( x k ) } + = 0 E { w k a ˉ k ( x k ) } + = 0 E { a ˉ k ( x k ) w k ⊤ } + E { w k w k ⊤ } = E { a ˉ k ( x k ) a ˉ k ⊤ ( x k ) } + E { w k w k ⊤ } = ∫ R N a k ( x k ) a k ⊤ ( x k ) f k e ( x k ) d x k + C k w Einschub: Konditionierung einer Gaußschen Verbunddichte Zufallsvektor z ‾ = [ x ‾ y ‾ ] \underline{z}=\left[\begin{array}{l}\underline{x} \\ \underline{y}\end{array}\right] z = [ x y ]
f ( z ‾ ) = N ( z ‾ 1 , z ^ ‾ , C z ) , z ^ ‾ = [ x ^ ‾ y ^ ‾ ] , C z = [ C x x C x y C y x C y y ]
f(\underline{z})=\mathcal{N}\left(\underline{z}_{1}, \underline{\hat{z}}, \mathbf{C}_{z}\right), \quad \underline{\hat{z}}=\left[\begin{array}{l}
\underline{\hat{x}} \\
\underline{\hat{y}}
\end{array}\right], \quad \mathbf{C}_{z}=\left[\begin{array}{ll}
C_{x x} & C_{x y} \\
C_{y x} & C_{y y}
\end{array}\right]
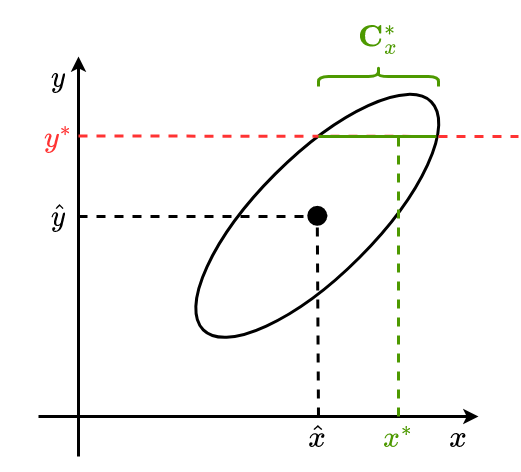
f ( z ) = N ( z 1 , z ^ , C z ) , z ^ = [ x ^ y ^ ] , C z = [ C xx C y x C x y C yy ] Gegeben: Messung y ∗ y^\ast y ∗
Konditionale Verteilung:
f ( x ‾ ∣ y ‾ ∗ ) = N ( x ‾ , x ^ ‾ ∗ , C x ∗ )
\begin{equation}
f\left(\underline{x} \mid \underline{y}^{\ast}\right)= \mathcal{N}\left(\underline{x}, \underline{\hat{x}}^{*}, \mathbf{C}_{x}^{\ast}\right)
\end{equation}
f ( x ∣ y ∗ ) = N ( x , x ^ ∗ , C x ∗ ) Dann ist
x ^ ‾ ∗ = x ^ ‾ + C x y C y y − 1 ( y ‾ ∗ − y ^ ‾ ) C x ∗ = C x x − C x y C y y − 1 C y x (*)
\begin{array}{l}
\underline{\hat{x}}^{\ast}=\underline{\hat{x}}+C_{x y} C_{y y}^{-1}\left(\underline{y}^{*}-\underline{\hat{y}}\right) \\
\mathbf{C}_{x}^{\ast}=C_{x x}-C_{x y} C_{y y}^{-1} C_{y x}
\end{array}
\tag{*}
x ^ ∗ = x ^ + C x y C yy − 1 ( y ∗ − y ^ ) C x ∗ = C xx − C x y C yy − 1 C y x ( * ) Alternative Herleitung Kalmanfilter Messmodell
y ‾ = H ⋅ x ‾ + v ‾
\underline{y}=\mathbf{H} \cdot \underline{x}+\underline{v}
y = H ⋅ x + v Gegeben:
x ‾ p ∼ N ( x ‾ ^ p , C p ) , v ‾ ∼ N ( 0 ‾ , C v )
\underline{x}_{p} \sim \mathcal{N}\left(\hat{\underline{x}}_{p}, \mathbf{C}_{p}\right), \quad \underline{v}\sim \mathcal{N}\left(\underline{0}, \mathbf{C}_{v}\right)
x p ∼ N ( x ^ p , C p ) , v ∼ N ( 0 , C v ) Wir definiere z ‾ \underline{z} z x ‾ p \underline{x}_{p} x p y ‾ \underline{y} y
z ‾ : = [ x ‾ p y ‾ ] = [ x ‾ p H ⋅ x ‾ p + v ‾ ] = [ I 0 H I ] [ x ‾ p v ‾ ]
\underline{z}:=\left[\begin{array}{l}
\underline{x}_{p} \\
\underline{y}
\end{array}\right]=\left[\begin{array}{l}
\underline{x}_{p} \\
\mathbf{H} \cdot \underline{x}_{p}+\underline{v}
\end{array}\right]=\left[\begin{array}{ll}
\mathbf{I} & 0 \\
\mathbf{H} & \mathbf{I}
\end{array}\right]\left[\begin{array}{c}
\underline{x}_{p} \\
\underline{v}
\end{array}\right]
z := [ x p y ] = [ x p H ⋅ x p + v ] = [ I H 0 I ] [ x p v ] Die Erwartungswert ist dann
z ^ ‾ = [ x ^ p H ⋅ x ^ p ]
\underline{\hat{z}}=\left[\begin{array}{c}
\hat{x}_{p} \\
\mathbf{H} \cdot \hat{x}_{p}
\end{array}\right]
z ^ = [ x ^ p H ⋅ x ^ p ] Die Kovairanzmatrix von z ‾ \underline{z} z
Cov { z ‾ } = E { [ I 0 H I ] [ x ‾ p − x ‾ ^ p v ‾ ] [ x ‾ p − x ^ ‾ p v ‾ ] ⊤ [ I H ⊤ 0 I ] } = [ I 0 H I ] E { [ ( x ‾ p − x ^ ‾ p ) ( x ‾ p − x ^ ‾ p ) ⊤ ⏟ = C p ( x ‾ p − x ^ ‾ p ) v ‾ ⊤ ⏟ = 0 v ‾ ( x ‾ p − x ^ ‾ p ) ⏟ = 0 v ‾ v ‾ ⊤ ⏟ = C v ] } [ I 0 H I ] = [ I 0 H I ] [ C p 0 0 C v ] [ I 0 H I ] = [ C p C p H ⊤ H C p C v + H C p H ⊤ ]
\begin{array}{l}
\operatorname{Cov}\{\underline{z}\}&=E\left\{\left[\begin{array}{ll}
\mathbf{I} & 0 \\
\mathbf{H} & \mathbf{I}
\end{array}\right]\left[\begin{array}{c}
\underline{x}_{p}-\hat{\underline{x}}_{p} \\
\underline{v}
\end{array}\right]\left[\begin{array}{c}
\underline{x}_{p}-\underline{\hat{x}}_{p} \\
\underline{v}
\end{array}\right]^{\top}\left[\begin{array}{cc}
\mathbf{I} & \mathbf{H}^{\top} \\
0 & \mathbf{I}
\end{array}\right]\right\}\\\\
&=\left[\begin{array}{ll}
\mathbf{I} & 0 \\
\mathbf{H} & \mathbf{I}
\end{array}\right] E\left\{\left[\begin{array}{cc}
\underbrace{\left(\underline{x}_{p}-\underline{\hat{x}}_{p}\right)(\underline{x}_{p}-\underline{\hat{x}}_{p})^{\top}}_{=\mathbf{C}_p} & \underbrace{\left(\underline{x}_{p}-\underline{\hat{x}}_{p}\right) \underline{v}^{\top}}_{=0} \\
\underbrace{\underline{v}\left(\underline{x}_{p}-\underline{\hat{x}}_{p}\right)}_{=0} & \underbrace{\underline{v} \underline{v}^{\top}}_{=\mathbf{C}_v}
\end{array}\right]\right\}\left[\begin{array}{cc}
\mathbf{I} & 0 \\
\mathbf{H} & \mathbf{I}
\end{array}\right]\\\\
&=\left[\begin{array}{ll}
\mathbf{I} & 0 \\
\mathbf{H} & \mathbf{I}
\end{array}\right]\left[\begin{array}{cc}
\mathbf{C}_p & 0 \\
0 & \mathbf{C}_v
\end{array}\right]\left[\begin{array}{cc}
\mathbf{I} & 0 \\
\mathbf{H} & \mathbf{I}
\end{array}\right]=\left[\begin{array}{cc}
\mathbf{C}_{p} & \mathbf{C}_{p} \mathbf{H}^{\top} \\
\mathbf{H} \mathbf{C}_{p} & \mathbf{C}_{v}+\mathbf{H} \mathbf{C}_{p} \mathbf{H}^{\top}
\end{array}\right]
\end{array}
Cov { z } = E { [ I H 0 I ] [ x p − x ^ p v ] [ x p − x ^ p v ] ⊤ [ I 0 H ⊤ I ] } = [ I H 0 I ] E ⎩ ⎨ ⎧ = C p ( x p − x ^ p ) ( x p − x ^ p ) ⊤ = 0 v ( x p − x ^ p ) = 0 ( x p − x ^ p ) v ⊤ = C v v v ⊤ ⎭ ⎬ ⎫ [ I H 0 I ] = [ I H 0 I ] [ C p 0 0 C v ] [ I H 0 I ] = [ C p H C p C p H ⊤ C v + H C p H ⊤ ] Lasse
C x x = C p C x y = C p H ⊤ C y x = H C p C y y = C v + H C p H ⊤
\mathbf{C}_{x x}=\mathbf{C}_{p} \quad \mathbf{C}_{x y}=\mathbf{C}_{p} \mathbf{H}^{\top} \quad \mathbf{C}_{y x}=\mathbf{H} \mathbf{C}_{p} \quad \mathbf{C}_{y y}=\mathbf{C}_{v}+\mathbf{H} \mathbf{C}_{p} \mathbf{H}^{\top}
C xx = C p C x y = C p H ⊤ C y x = H C p C yy = C v + H C p H ⊤ und in ( ∗ ) (*) ( ∗ )
Messgleichung
y ‾ = h ‾ ( x ‾ , v ‾ )
\underline{y}=\underline{h}(\underline{x}, \underline{v})
y = h ( x , v ) Definiere
z ‾ = [ x ‾ y ‾ ] = [ x ‾ h ‾ ( x ‾ , v ‾ ) ] ⇒ E { z ‾ } = [ x ^ ‾ p E { h ‾ ( x ‾ , v ‾ ) } ]
\underline{z}=\left[\begin{array}{l}
\underline{x} \\
\underline{y}
\end{array}\right]=\left[\begin{array}{c}
\underline{x} \\
\underline{h}(\underline{x}, \underline{v})
\end{array}\right] \Rightarrow E\{\underline{z}\}=\left[\begin{array}{c}
\underline{\hat{x}}_{p} \\
E\{\underline{h}(\underline{x}, \underline{v})\}
\end{array}\right]
z = [ x y ] = [ x h ( x , v ) ] ⇒ E { z } = [ x ^ p E { h ( x , v )} ] Bei additivem Rauschen
y = h ‾ ( x ‾ ) + v ‾
y=\underline{h}(\underline{x})+\underline{v}
y = h ( x ) + v gilt
E { z ‾ } = [ x ^ ‾ p E { h ‾ ( x ) } ] , E { h ‾ ( x ) } = ∫ R N h ‾ ( x ) f p ( x ) ⏟ = N ( x ‾ , x ^ ‾ p , C p ) d x ‾ ∈ R M
E\{\underline{z}\}=\left[\begin{array}{c}
\underline{\hat{x}}_{p} \\
E\{\underline{h}(x)\}
\end{array}\right], \quad E\{\underline{h}(x)\}=\int_{\mathbb{R}^{N}} \underline{h}(x) \underbrace{f_{p}(x)}_{= \mathcal{N}(\underline{x}, \underline{\hat{x}}_{p}, \mathbf{C}_p)} d \underline{x} \in \mathbb{R}^{M}
E { z } = [ x ^ p E { h ( x )} ] , E { h ( x )} = ∫ R N h ( x ) = N ( x , x ^ p , C p ) f p ( x ) d x ∈ R M Kovarianzmatrix:
E { ( x ‾ − x ^ ‾ p ) } h ˉ ‾ ⊤ ( x ‾ ) = ∫ R N ( x ‾ − x ^ ‾ p ) h ˉ ‾ ⊤ f p ( x ‾ ) d x ‾ ∈ R N × M
E\left\{\left(\underline{x}-\underline{\hat{x}}_{p}\right)\right\} \underline{\bar{h}}^{\top}(\underline{x}) = \int_{\mathbb{R}^N} (\underline{x}-\underline{\hat{x}}_{p}) \underline{\bar{h}}^{\top} f_p(\underline{x}) d\underline{x} \in \mathbb{R}^{N \times M}
E { ( x − x ^ p ) } h ˉ ⊤ ( x ) = ∫ R N ( x − x ^ p ) h ˉ ⊤ f p ( x ) d x ∈ R N × M E { h ˉ ‾ ( x ) h ˉ ‾ ⊤ ( x ‾ ) } = ∫ R N h ˉ ‾ ( x ) h ˉ ‾ ⊤ ( x ‾ ) f p ( x ‾ ) d x ‾ ∈ R M × M
E\left\{\underline{\bar{h}}(x) \underline{\bar{h}}^{\top}(\underline{x})\right\} = \int_{\mathbb{R}^N} \underline{\bar{h}}(x) \underline{\bar{h}}^{\top}(\underline{x}) f_p(\underline{x}) d\underline{x} \in \mathbb{R}^{M \times M}
E { h ˉ ( x ) h ˉ ⊤ ( x ) } = ∫ R N h ˉ ( x ) h ˉ ⊤ ( x ) f p ( x ) d x ∈ R M × M Cov { z ‾ } = [ C x x ⏞ R N × N C x y ⏞ R N × M C y x ⏟ R M × N C y y ⏟ R M × M ] ∈ R ( N + M ) × ( N + M )
\operatorname{Cov}\{\underline{z}\}=\left[\begin{array}{ll}
\overbrace{C_{x x}}^{\mathbb{R}^{N \times N}} & \overbrace{C_{x y}}^{\mathbb{R}^{N \times M}}\\
\underbrace{C_{y x}}_{\mathbb{R}^{M \times N}} & \underbrace{C_{y y}}_{\mathbb{R}^{M \times M}}
\end{array}\right] \in R^{(N+M) \times (N+M)}
Cov { z } = C xx R N × N R M × N C y x C x y R N × M R M × M C yy ∈ R ( N + M ) × ( N + M ) Einsetzen in ( ∗ ) (\ast) ( ∗ ) Nichtlineare Kalman Filter :
x ^ ‾ e = x ^ ‾ p + C x y C y y − 1 ( y ^ ‾ − E { h ‾ ( x ‾ ) } ) C e = C p − C x y C y y − 1 C y x
\begin{array}{l}
\underline{\hat{x}}_{e}=\underline{\hat{x}}_{p}+\mathbf{C}_{x y} \mathbf{C}_{y y}^{-1}(\underline{\hat{y}}-E\{\underline{h}(\underline{x})\}) \\
\mathbf{C}_{e}=\mathbf{C}_{p}-\mathbf{C}_{x y} \mathbf{C}_{y y}^{-1} \mathbf{C}_{y x}
\end{array}
x ^ e = x ^ p + C x y C yy − 1 ( y ^ − E { h ( x )}) C e = C p − C x y C yy − 1 C y x