Statische und Dynamische Systeme
Statische Systeme
Ein-/Ausgang: Zufallsvektoren und ( ist der Zeitschritt)
- und sind wertekontinuierlich
Abbildung von und durch nichtlineare Abbildung
Beschreibung der Unsicherheit in und durch Dichten
- :
- :
Gesucht: zu gegeben
Dynamische Systeme
Systemabbildung
Zustand mit
Nichtlineare System (allg.)
Beschreibung von durch Dichte
Spezielle Rauschstruktur: Additives Rauschen
Systemrauschen wird beschrieben durch Dichte
Typische Annahme
ist Gauß verteilt mit bekannten Parametern
ist weißes Rauschen
White noise: uncertainties taken at different time steps are independent
Messabbildung
Nichtlineare Abbildung (allg.)
Spezialfall: Additives Rauschen
Rauschen beschrieben durch
Gesammtsystem
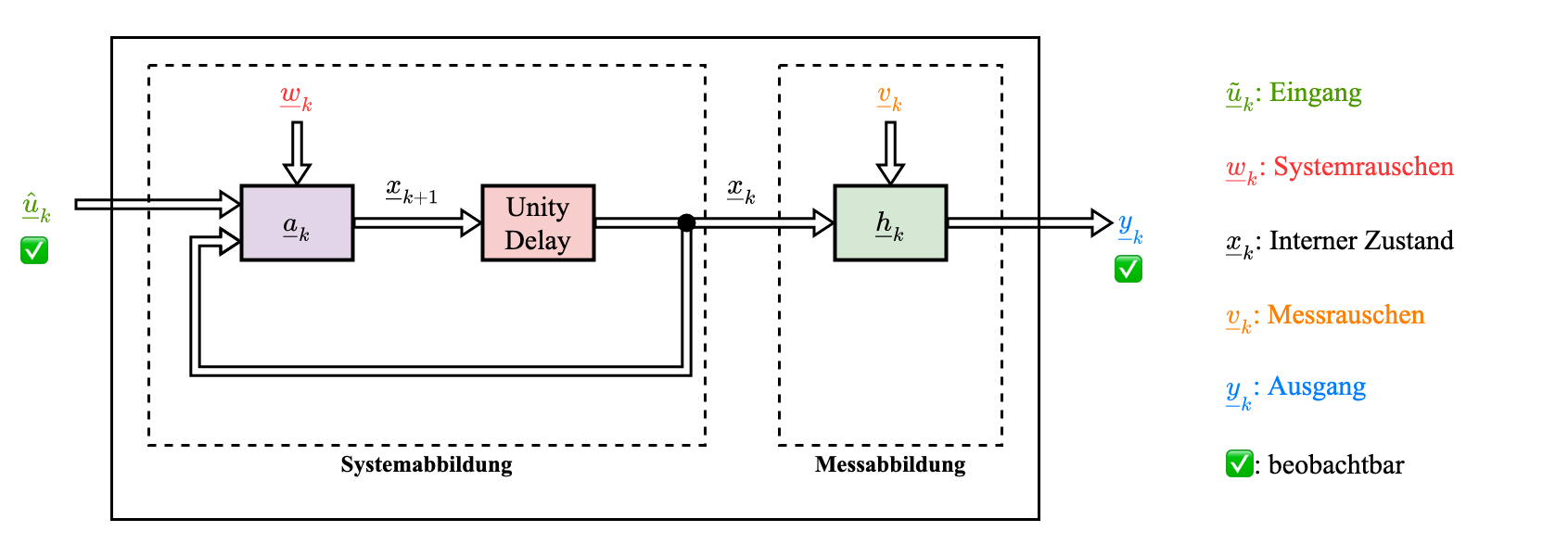
Note: Das System ist gekapselt. Von außen können wir nur
und
sehen.
Lineare Vs. Nichtlineare Systeme
| Linear | Nichtlinear | |
|---|---|---|
| Systemabbildung | ||
| Messabbildung |