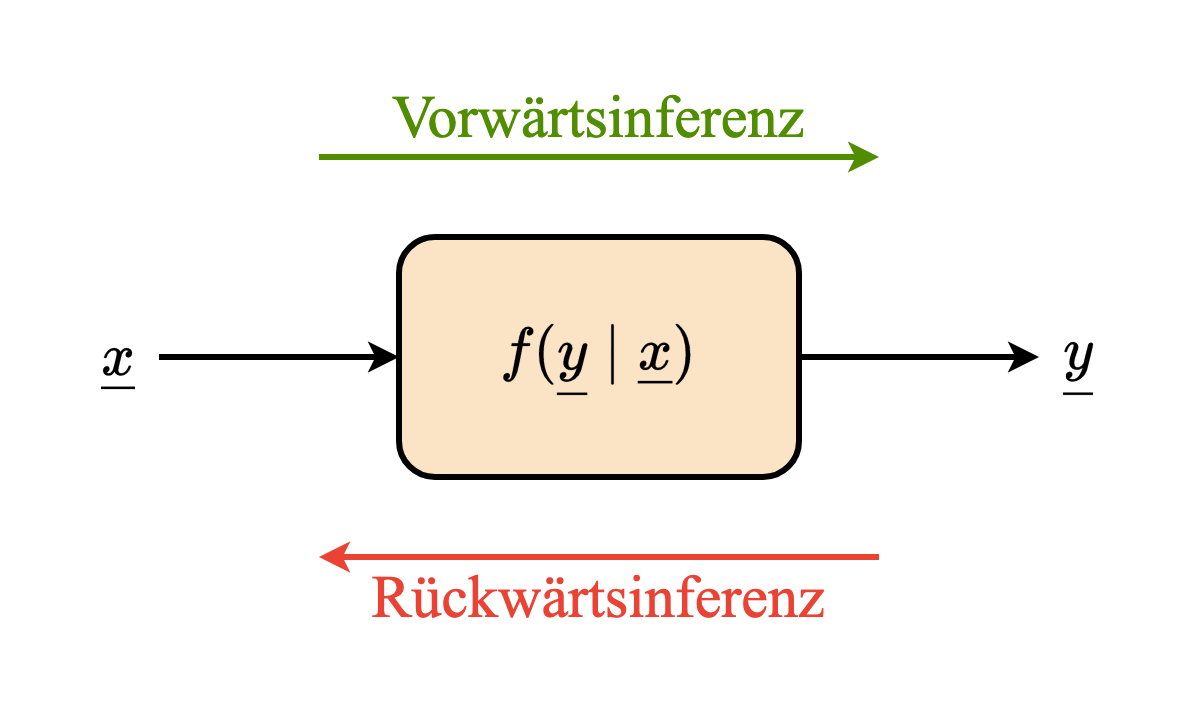
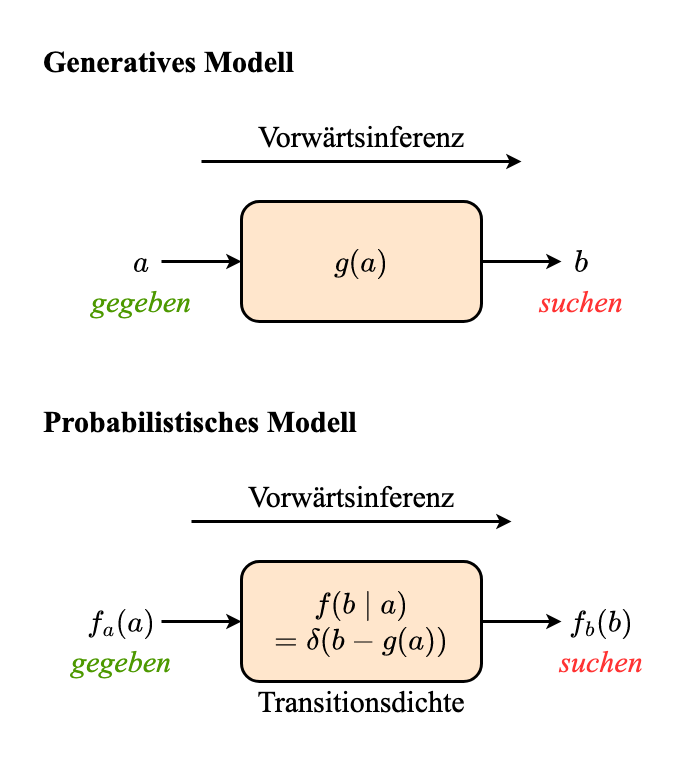
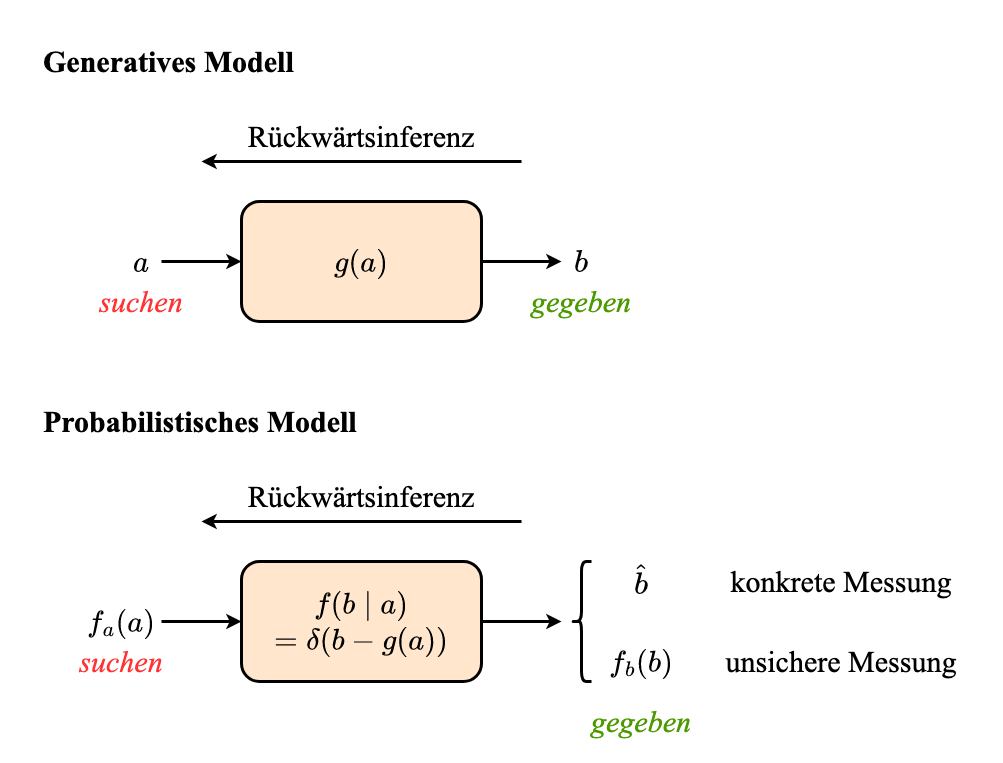
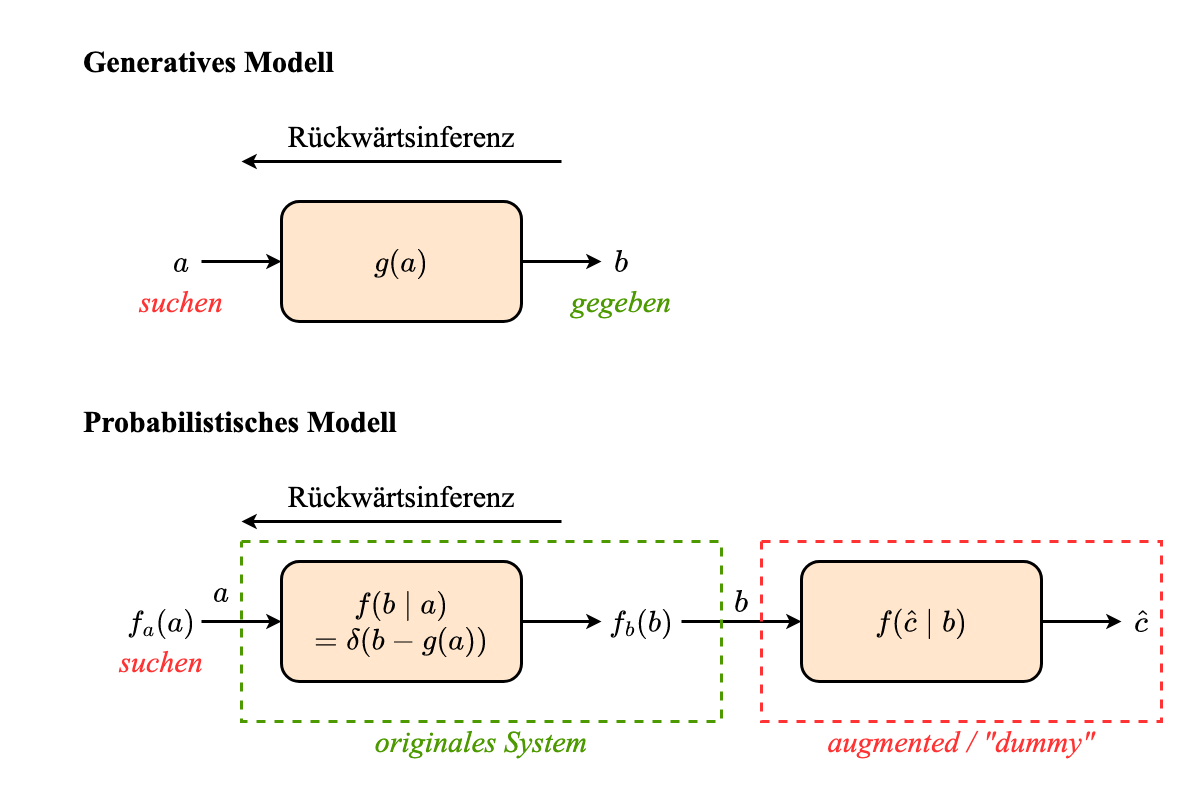
Allgemeine Systeme Generatives und probabilistisches Modell Für Herleitung ist es super wichtig, die Eigenschaft der Dirac’schen Funktion anzuwenden:
δ ( g ( x ) ) = ∑ i = 1 N 1 ∣ g ′ ( x i ) ∣ δ ( x − x i )
\delta (g(x)) = \sum_{i=1}^N \frac{1}{|g^\prime(x_i)|}\delta (x - x_i)
δ ( g ( x )) = i = 1 ∑ N ∣ g ′ ( x i ) ∣ 1 δ ( x − x i ) g ( x i ) = 0 g(x_i) = 0 g ( x i ) = 0 g ′ ( x i ) ≠ 0 g^\prime(x_i) \neq 0 g ′ ( x i ) = 0 Mit Additivem Rauschen Generatives Modell:
z = a ( x ) + v v ∼ f v ( v )
z = a(x) + v \quad v \sim f_v(v)
z = a ( x ) + v v ∼ f v ( v ) Probabilistisches Modell:
f ( z ∣ x ) = f v ( z − a ( x ) )
f(z \mid x) = f_v(z - a(x))
f ( z ∣ x ) = f v ( z − a ( x )) Mit Multiplikativem Rauschen Generatives Modell:
z = x ⋅ v v ∼ f v ( v )
z = x \cdot v \quad v \sim f_v(v)
z = x ⋅ v v ∼ f v ( v ) Probabilistisches Modell:
f ( z ∣ x ) = 1 ∣ x ∣ f v ( z x )
f(z \mid x) = \frac{1}{|x|}f_v(\frac{z}{x})
f ( z ∣ x ) = ∣ x ∣ 1 f v ( x z ) Warum lässt sich das nur bei bestimmten Modellen exakt lösen? “For the general generative model, where the noise enters the system in an arbitrary fashion.” (Script P149)
Abstraktion Prädiktion (Vorwärtsinferenz) Gegebenf a ( a ) f_a(a) f a ( a ) g ( a ) g(a) g ( a ) Gesucht: f b ( b ) f_b(b) f b ( b ) Chapman-Kolmogorov-Gleichung f k + 1 p ( x ‾ k + 1 ) = ∫ R N f ( x ‾ k + 1 ∣ x ‾ k ) ⏟ Pr a ¨ diktionsdichte f k e ( x ‾ k ) d x ‾ k
f_{k+1}^{p}\left(\underline{x}_{k+1}\right)=\int_{\mathbb{R}^{N}} \underbrace{f\left(\underline{x}_{k+1} \mid \underline{x}_{k}\right)}_{\text{Prädiktionsdichte}} f_{k}^{e}\left(\underline{x}_{k}\right) \mathrm{d} \underline{x}_{k}
f k + 1 p ( x k + 1 ) = ∫ R N Pr a ¨ diktionsdichte f ( x k + 1 ∣ x k ) f k e ( x k ) d x k Herleitung ist ganz simple: Verbunddichte + Marginalisierung
f ( x k + 1 ) = ∫ R N f ( x ‾ k + 1 , x ‾ k ) d x ‾ k = ∫ R N f ( x ‾ k + 1 ∣ x ‾ k ) ⋅ f ( x ‾ k ) d x ‾ k
f\left(x_{k+1}\right)= \int_{\mathbb{R}^{N}} f\left(\underline{x}_{k+1}, \underline{x}_{k}\right) d \underline{x}_{k}= \int_{\mathbb{R}^{N}} f\left(\underline{x}_{k+1} \mid \underline{x}_{k}\right) \cdot f\left(\underline{x}_{k}\right) d \underline{x}_{k}
f ( x k + 1 ) = ∫ R N f ( x k + 1 , x k ) d x k = ∫ R N f ( x k + 1 ∣ x k ) ⋅ f ( x k ) d x k ‼️ Problem: Parameterintegral
Integrand hängt von x ‾ k + 1 \underline{x}_{k+1} x k + 1 Erfordert Lösung des Integrals für alle x ‾ k + 1 \underline{x}_{k+1} x k + 1 Nur möglich für analytische Lösung Prädiktionsschritte Umforme f ( b ∣ a ) = δ ( b − g ( a ) ) f(b \mid a) = \delta(b - g(a)) f ( b ∣ a ) = δ ( b − g ( a ))
δ ( g ( x ) ) = ∑ i = 1 N 1 ∣ g ′ ( x i ) ∣ δ ( x − x i )
\delta (g(x)) = \sum_{i=1}^N \frac{1}{|g^\prime(x_i)|}\delta (x - x_i)
δ ( g ( x )) = i = 1 ∑ N ∣ g ′ ( x i ) ∣ 1 δ ( x − x i ) wobei
g ( x i ) = 0 g(x_i) = 0 g ( x i ) = 0 x i x_i x i i = 1 , 2 , … , N i = 1, 2, \dots, N i = 1 , 2 , … , N g ′ ( x i ) ≠ 0 g^\prime(x_i) \neq 0 g ′ ( x i ) = 0 Berechne f b ( b ) f_b(b) f b ( b ) Chapman-Kolmogorov-Gleichung
f ( b ) = ∫ f ( b ∣ a ) f ( a ) d a
f(b) = \int f(b \mid a) f(a) da
f ( b ) = ∫ f ( b ∣ a ) f ( a ) d a und setze die Unformung von f ( b ∣ a ) f(b \mid a) f ( b ∣ a ) f b ( b ) f_b(b) f b ( b ) f a ( a ) f_a(a) f a ( a )
Vereinfachte Prädiktion Für
z ‾ = a ‾ ( x ‾ , w ‾ )
\underline{z} = \underline{a}(\underline{x}, \underline{w})
z = a ( x , w ) ist die Transitionsdichte f ( z ‾ ∣ x ‾ ) f(\underline{z} | \underline{x}) f ( z ∣ x )
f ( z ‾ ∣ x ‾ ) = ∑ i ∈ Z f i z ( z ‾ ) ⋅ f i x ( x ‾ )
f(\underline{z} | \underline{x}) = \sum_{i \in \mathbb{Z}} f_i^z(\underline{z}) \cdot f_i^x(\underline{x})
f ( z ∣ x ) = i ∈ Z ∑ f i z ( z ) ⋅ f i x ( x ) wobei f i z ( z ‾ ) f_i^z(\underline{z}) f i z ( z ) f i x ( x ‾ ) f_i^x(\underline{x}) f i x ( x )
Schreibweise mit x ‾ k + 1 \underline{x}_{k+1} x k + 1 x ‾ k \underline{x}_{k} x k
f ( x ‾ k + 1 ∣ x ‾ k ) = ∑ i = 1 L w k ( i ) f k + 1 ( i ) ( x ‾ k + 1 ) f k ( i ) ( x ‾ k )
f\left(\underline{x}_{k+1} \mid \underline{x}_k\right)=\sum_{i=1}^L w_k^{(i)} f_{k+1}^{(i)}\left(\underline{x}_{k+1}\right) f_k^{(i)}\left(\underline{x}_k\right)
f ( x k + 1 ∣ x k ) = i = 1 ∑ L w k ( i ) f k + 1 ( i ) ( x k + 1 ) f k ( i ) ( x k ) Filterung Rückwartsinferenz Bei Rückwartsinferenz ist es wichtig, Formel von Bayes anwuwenden.
f ( a ∣ b ) = f ( a , b ) f ( b ) = f ( b ∣ a ) f ( a ) f ( b ) = 1 f ( b ) ⏟ Normalizationskonstant ⋅ f ( b ∣ a ) ⏟ Likelihood ⋅ f ( a ) ⏟ Vorwissen
f(a \mid b) = \frac{f(a, b)}{f(b)} = \frac{f(b \mid a) f(a)}{f(b)} = \underbrace{\frac{1}{f(b)}}_{\text{Normalizationskonstant}} \cdot \underbrace{f(b \mid a)}_{\text{Likelihood}} \cdot \underbrace{f(a)}_{\text{Vorwissen}}
f ( a ∣ b ) = f ( b ) f ( a , b ) = f ( b ) f ( b ∣ a ) f ( a ) = Normalizationskonstant f ( b ) 1 ⋅ Likelihood f ( b ∣ a ) ⋅ Vorwissen f ( a ) Konkrete Messung Umforme f b ( b ∣ a ) = δ ( b − g ( a ) ) f_b(b \mid a) = \delta(b - g(a)) f b ( b ∣ a ) = δ ( b − g ( a ))
δ ( g ( x ) ) = ∑ i = 1 N 1 ∣ g ′ ( x i ) ∣ δ ( x − x i )
\delta (g(x)) = \sum_{i=1}^N \frac{1}{|g^\prime(x_i)|}\delta (x - x_i)
δ ( g ( x )) = i = 1 ∑ N ∣ g ′ ( x i ) ∣ 1 δ ( x − x i ) wobei
g ( x i ) = 0 g(x_i) = 0 g ( x i ) = 0 x i x_i x i i = 1 , 2 , … , N i = 1, 2, \dots, N i = 1 , 2 , … , N g ′ ( x i ) ≠ 0 g^\prime(x_i) \neq 0 g ′ ( x i ) = 0 Berechne f b ( b ) f_b(b) f b ( b )
f b ( b ) = ∫ f a , b ( a , b ) d a = ∫ f b ( b ∣ a ) f a ( a ) d a
f_b(b) = \int f_{a, b}(a, b) da = \int f_{b}(b \mid a) f_a(a) da
f b ( b ) = ∫ f a , b ( a , b ) d a = ∫ f b ( b ∣ a ) f a ( a ) d a mit Einsetzen der Unformung von f ( b ∣ a ) f(b \mid a) f ( b ∣ a )
Berechne f a ( a ∣ b ^ ) f_a(a \mid \hat{b}) f a ( a ∣ b ^ )
f a ( a ∣ b ^ ) = f a ( b ^ ∣ a ) f a ( a ) f b ( b ^ ) = δ ( b ^ − g ( a ) ) ⏞ Schritt 1 f a ( a ) f b ( b ^ ) ⏟ Schritt 2
f_a(a \mid \hat{b}) = \frac{f_a(\hat{b} \mid a) f_a(a)}{f_b(\hat{b})} = \frac{\overbrace{\delta(\hat{b} - g(a))}^{\text{Schritt 1}} f_a(a)}{\underbrace{f_b(\hat{b})}_{\text{Schritt 2}}}
f a ( a ∣ b ^ ) = f b ( b ^ ) f a ( b ^ ∣ a ) f a ( a ) = Schritt 2 f b ( b ^ ) δ ( b ^ − g ( a )) Schritt 1 f a ( a ) Unsichere Messung Schritte :
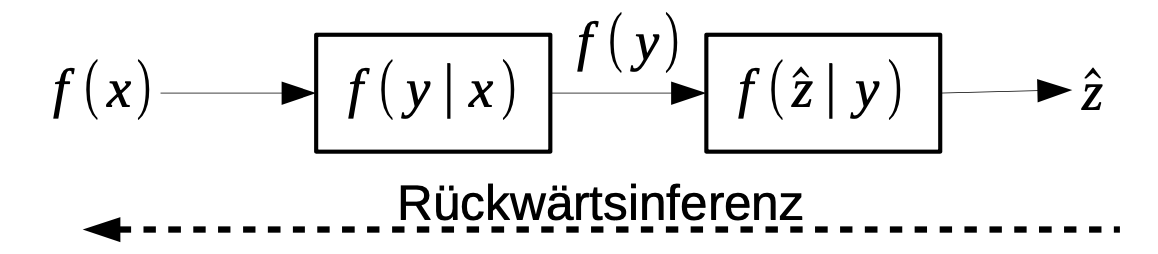
Erweitere das System um eine zusätzliche stochastische Abbildung und einen festen Ausgang z ^ \hat{z} z ^ Bestimme f ( z ^ ∣ y ) f(\hat{z} \mid y) f ( z ^ ∣ y )
f ( z ^ ∣ y ) = f ( y ∣ z ^ ) f ( z ^ ) f ( y ) = f ( y ∣ z ^ ) f ( z ^ ) ∫ f ( y , x ) d x = f ( y ∣ z ^ ) f ( z ^ ) ∫ f ( y ∣ x ) f ( x ) d x = f ( y ∣ z ^ ) f ( z ^ ) ∫ δ ( y − g ( x ) ) f ( x ) d x
\begin{aligned}
f(\hat{z} \mid y) &= \frac{f(y \mid \hat{z})f(\hat{z})}{f(y)} \\\\
&= \frac{f(y \mid \hat{z})f(\hat{z})}{\int f(y, x) dx} \\\\
&= \frac{f(y \mid \hat{z})f(\hat{z})}{\int f(y|x)f(x) dx} \\\\
&= \frac{f(y \mid \hat{z})f(\hat{z})}{\int \delta(y - g(x)) f(x) dx} \\\\
\end{aligned}
f ( z ^ ∣ y ) = f ( y ) f ( y ∣ z ^ ) f ( z ^ ) = ∫ f ( y , x ) d x f ( y ∣ z ^ ) f ( z ^ ) = ∫ f ( y ∣ x ) f ( x ) d x f ( y ∣ z ^ ) f ( z ^ ) = ∫ δ ( y − g ( x )) f ( x ) d x f ( y ∣ z ^ ) f ( z ^ ) Und setze die Umformung von δ ( y − g ( x ) ) \delta(y - g(x)) δ ( y − g ( x ))
δ ( g ( x ) ) = ∑ i = 1 N 1 ∣ g ′ ( x i ) ∣ δ ( x − x i )
\delta (g(x)) = \sum_{i=1}^N \frac{1}{|g^\prime(x_i)|}\delta (x - x_i)
δ ( g ( x )) = i = 1 ∑ N ∣ g ′ ( x i ) ∣ 1 δ ( x − x i ) g ( x i ) = 0 g(x_i) = 0 g ( x i ) = 0 x i x_i x i i = 1 , 2 , … , N i = 1, 2, \dots, N i = 1 , 2 , … , N g ′ ( x i ) ≠ 0 g^\prime(x_i) \neq 0 g ′ ( x i ) = 0 ein.
Berechung der Rückwärtsinferenz f ( x ∣ z ^ ) f(x \mid \hat{z}) f ( x ∣ z ^ )
f ( x ∣ z ^ ) = 1 f ( z ^ ) ⋅ f ( x , z ^ ) ∣ Marginalisierung nach y = 1 f ( z ^ ) ∫ f ( x , y , z ^ ) d y = 1 f ( z ^ ) ∫ f ( z ^ ∣ y , x ) ⋅ f ( y , x ) d y ∣ z ^ , x sind unabh a ¨ ngig = 1 f ( z ^ ) ∫ f ( z ^ ∣ y ) ⋅ f ( y ∣ x ) ⋅ f ( x ) d y = 1 f ( z ^ ) ∫ f ( z ^ ∣ y ) ⏟ Berechnet in Schritt 1 ⋅ f ( y ∣ x ) ⏟ Systemmodell ⋅ f ( x ) d y
\begin{aligned}
f(x \mid \hat{z}) &=\frac{1}{f\left(\hat{z}\right)} \cdot f(x, \hat{z}) \quad \mid \text{Marginalisierung nach } y\\
&=\frac{1}{f(\hat{z})} \int f(x, y, \hat{z}) d y \\
&=\frac{1}{f(\hat{z})} \int f(\hat{z} \mid y, x) \cdot f(y , x) d y \quad \mid \hat{z}, x \text{ sind unabhängig}\\
&=\frac{1}{f(\hat{z})} \int f(\hat{z} \mid y) \cdot f(y \mid x) \cdot f(x) d y \\
&=\frac{1}{f(\hat{z})} \int \underbrace{f(\hat{z} \mid y)}_{\text{Berechnet in Schritt 1}} \cdot \underbrace{f(y \mid x)}_{\text{Systemmodell}} \cdot f(x) d y
\end{aligned}
f ( x ∣ z ^ ) = f ( z ^ ) 1 ⋅ f ( x , z ^ ) ∣ Marginalisierung nach y = f ( z ^ ) 1 ∫ f ( x , y , z ^ ) d y = f ( z ^ ) 1 ∫ f ( z ^ ∣ y , x ) ⋅ f ( y , x ) d y ∣ z ^ , x sind unabh a ¨ ngig = f ( z ^ ) 1 ∫ f ( z ^ ∣ y ) ⋅ f ( y ∣ x ) ⋅ f ( x ) d y = f ( z ^ ) 1 ∫ Berechnet in Schritt 1 f ( z ^ ∣ y ) ⋅ Systemmodell f ( y ∣ x ) ⋅ f ( x ) d y Schwierigkeit vom Filterschritt Type der Dichte zur Beschreibung der Schätzung ändert sich Dichte wrid mit jedem Schritt komplexer Vereinfachte Filterung Vereinfachung der Likelihood f ( y ‾ ∣ x ‾ ) f(\underline{y} \mid \underline{x}) f ( y ∣ x )
f ( y ‾ ∣ x ‾ ) = ∑ i ∈ Z f i y ( y ‾ ) f i x ( x ‾ )
f(\underline{y} \mid \underline{x}) = \sum_{i \in \mathbb{Z}} f_i^y(\underline{y}) f_i^x(\underline{x})
f ( y ∣ x ) = i ∈ Z ∑ f i y ( y ) f i x ( x )