Sampling
Reapproximation von Dichten
Approximate original continuous density with discrete Dirac Mixture
$$ f(\underline{x})=\sum_{i=1}^{L} w_{i} \cdot \delta\left(\underline{x}-\underline{\hat{x}}_{i}\right) $$- Weights $w_{i}>0, \displaystyle \sum_{i=1}^{L} w_{i}=1$
- $\underline{x}_i$: locations / samples
In univariate case (1D), compare cumulative distribution functions (CDFs) $\tilde{F}(x), F(x)$ using Cramér–von Mises distance:
$$ D(\underline{\hat{x}})=\int_{\mathbb{R}}(\tilde{F}(x)-F\left(x, \underline{\hat{x}})\right)^{2} \mathrm{~d} x $$$F(x, \underline{\hat{x}})$ : Dirac mixture cumulative distribution
$$ F(x, \underline{\hat{x}})=\sum_{i=1}^{L} w_{i} \mathrm{H}\left(x-\hat{x}_{i}\right) \text { with } \mathrm{H}(x)=\int_{-\infty}^{x} \delta(t) \mathrm{d} t= \begin{cases}0 & x<0 \\ \frac{1}{2} & x=0 \\ 1 & x>0\end{cases} $$with the Dirac position
$$ \underline{\hat{x}}=\left[\hat{x}_{1}, \hat{x}_{2}, \ldots, \hat{x}_{L}\right]^{\top} $$We minimize the Cramér–von Mises distance $D(\underline{\hat{x}})$ with Newton’s method.
Generalization of concept of CDF
Localized Cumulative Distribution (LCD)
$$ F(\underline{m}, b)=\int_{\mathbb{R}^{N}} f(\underline{x}) K(\underline{x}-\underline{m}, b) \mathrm{d} \underline{x} $$$K(\cdot, \cdot)$: Kernel
$$ K(\underline{x}-\underline{m}, b)=\prod_{k=1}^{N} \exp \left(-\frac{1}{2} \frac{\left(x_{k}-m_{k}\right)^{2}}{b^{2}}\right) $$$\underline{m}$: Kernel location
$\underline{b}$: Kernel width
Properties of LCD:
- Symmetric
- Unique
- Multivariate
Generalized Cramér–von Mises Distance (GCvD)
$$ D=\int_{\mathbb{R}_{+}} w(b) \int_{\mathbb{R}^{N}}(\tilde{F}(\underline{m}, b)-F(\underline{m}, b))^{2} \mathrm{~d} \underline{m} \mathrm{~d} b $$- $\tilde{F}(\underline{m}, b)$: LCD of continuous density
- $F(\underline{m}, b)$: LCD of Dirac mixture
Minimization of GCvD: Quasi-Newton method (L-BFGS)
Projected Cumulative Distribution (PCD)
Use reapproximation methods for univariate case in multivariate case.
Radon Transform
Represent general $N$-dimensional probability density functions via the set of all one-dimensional projections
Linear projection of random vector $\underline{\boldsymbol{x}} \in \mathbb{R}^{N}$ to to scalar random variable $\boldsymbol{r} \in \mathbb{R}$ onto line described by unit vector $\underline{u} \in \mathbb{S}^{N-1}$
$$ \boldsymbol{r} = \underline{u}^\top \underline{\boldsymbol{x}} $$Given probability density function $f(\underline{x})$ of random vector $\underline{\boldsymbol{x}}$, density $f_r(r \mid \underline{u})$ is Radon transfrom of $f(\underline{x})$ for all $\underline{u} \in \mathbb{S}^{N-1}$
$$ f_{r}(r \mid \underline{u})=\int_{\mathbb{R}^{N}} f(\underline{t}) \delta\left(r-\underline{u}^{\top} \underline{t}\right) \mathrm{d} \underline{t} $$
Representing PDFs by all one-dimensional projections
Represent the two densities $\tilde{f}(\underline{x})$ and $f(\underline{x})$ by their Radon transforms $\tilde{f}(r \mid \underline{u})$ and $f(r \mid u)$
Compare the sets of projections $\tilde{f}(r \mid \underline{u})$ and $f(r \mid u)$ for every $\underline{u} \in \mathbb{S}^{N-1}$. Resulting distance is
$$ D_{1}(\underline{u})=D(\tilde{f}(r \mid \underline{u}), f(r \mid \underline{u})) $$Integrate these one-dimensional distance measures $D_1(\underline{u})$ over all unit vectors $\underline{u} \in \mathbb{S}^{N-1}$ to get the multivariate distance measure $D(\tilde{f}(\underline{x}), f(\underline{x}))$. Minimize via univariate Newton updates.
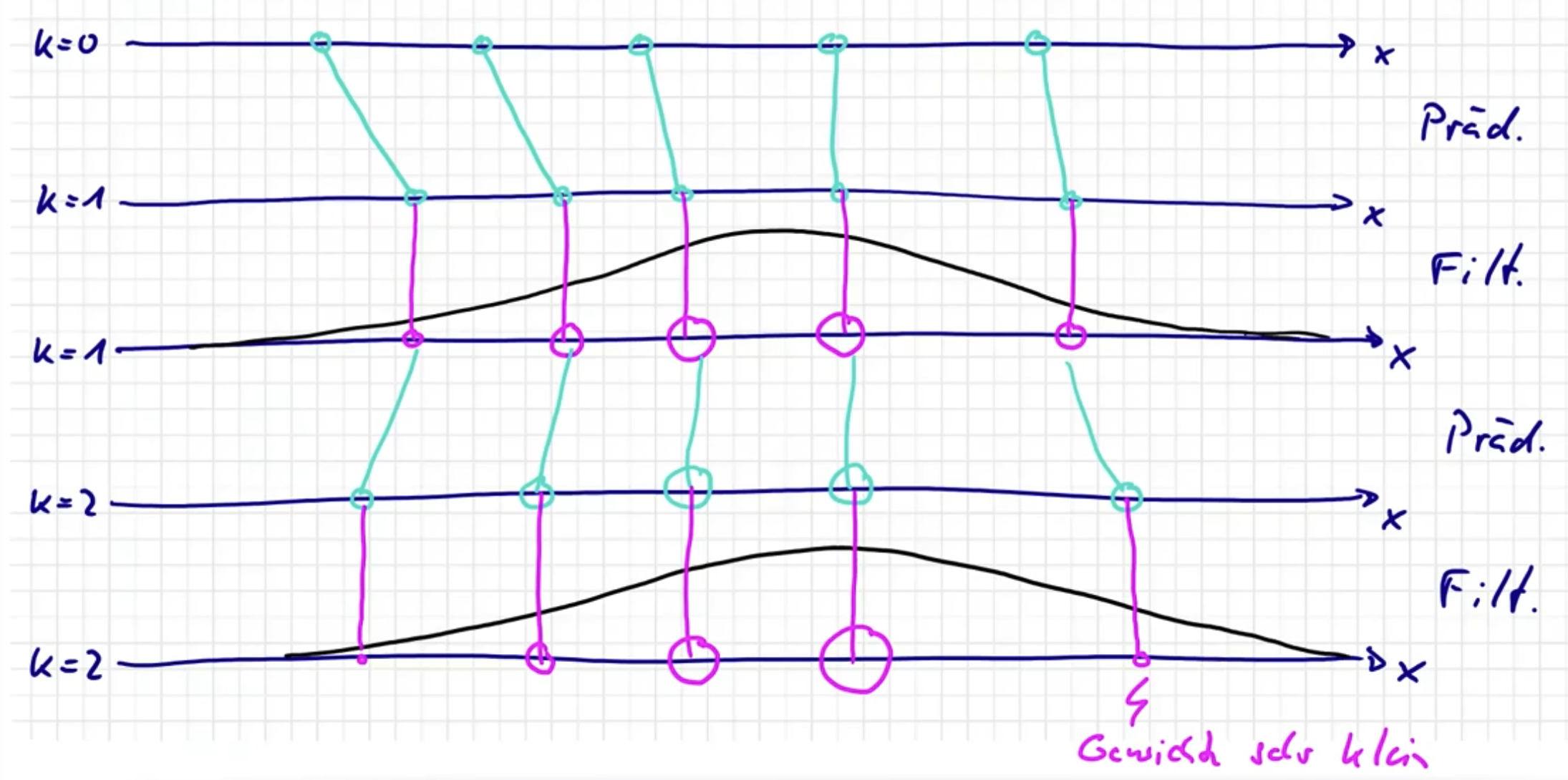
Navies Partikel Filter
Prädiktion
💡Update Sample Positionen. Gewichte bleiben gleich.
$f_{k}^{e}\left(\underline{x}_{k}\right)$ durch Dirac Mixture darstellen
$$ f_{k}^{e}\left(\underline{x}_{k}\right)=\sum_{i=1}^{L} w_{k}^{e, i} \cdot \delta\left(\underline{x}_{k}-\underline{\hat{x}}_{k}^{e, i}\right) \qquad w_{k}^{e, i}=\frac{1}{L}, i \in\left\{1, \ldots, L\right\} $$Ziehe Samples zum Zeitpunkt $k+1$
$$ \underline{\hat{x}}_{k+1}^{p, i} \sim f\left(\underline{x}_{k+1} \mid \hat{x}_{k}^{e, i}\right) $$Gewichte bleiben gleich
$$ w_{k+1}^{p, i} = w_{k}^{e, i} $$$f_{k+1}^{p}\left(\underline{x}_{k}\right)$ durch Dirac Mixture darstellen
$$ f_{k+1}^{p}\left(\underline{x}_{k+1}\right)=\sum_{i=1}^{L} w_{k+1}^{p, i} \delta\left(\underline{x}_{k+1}-\underline{\hat{x}}_{k+1}^{p, i}\right) $$
Filterung
💡Update Gewichte. Sample Positionen bleiben gleich.
$$ \begin{aligned} f_{k}^{e}\left(\underline{x}_{k}\right) &\propto f\left(\underline{y}_{k} \mid \underline{x}_{k}\right) \cdot f_{k}^{p}\left(\underline{x}_{k}\right)\\ &=f\left(\underline{y}_{k} \mid \underline{x}_{k}\right) \cdot \sum_{i=1}^{L} w_{k}^{p, i} \cdot \delta\left(\underline{x}_{k}-\underline{\hat{x}}_{k}^{p, i}\right)\\ &=\sum_{i=1}^{L} \underbrace{w_{k}^{p, i} \cdot f\left(\underline{y}_{k} \mid \hat{\underline{x}}_{k}^{p, i}\right)}_{\propto w_{k}^{e, i}} \cdot \delta(\underline{x}_{k}-\underbrace{\underline{\hat{x}}_{k}^{p, i}}_{\underline{\hat{x}}_{k}^{e, i}}) \end{aligned} $$Positionen bleiben gleich
$$ \underline{\hat{x}}_{k}^{e, i} = \underline{\hat{x}}_{k}^{p, i} $$Gewichte adaptieren
$$ w_{k}^{e, i} \propto w_{k}^{p, i} \cdot f\left(\underline{y}_{k} \mid \hat{\underline{x}}_{k}^{p, i}\right) $$und Normalisieren
$$ w_{k}^{e, i}:=\frac{w_{k}^{e, i}}{\displaystyle \sum_{i} w_{k}^{e,i}} $$
Problem
Varianz der Samples erhöht sich mit Filterschritten
Partikel sterben aus $\rightarrow$ Degenerierung des Filters
Aussterben schneller, je genauer die Messung, da Likelihood schmaler (Paradox!)
Resampling
Approximation der gewichteter Samples durch ungewichtete
$$ f_{k}^{e}\left(\underline{x}_{k}\right)=\sum_{i=1}^{L} w_{k}^{e, i} \cdot \delta\left(\underline{x}_{k}-\underline{\hat{x}}_{k}^{e, i}\right) \approx \sum_{i=1}^{L} \frac{1}{L} \delta\left(\underline{x}_{k}-\underline{\hat{x}}_{k}^{e, i}\right) $$Gegeben: $L$ Partikel mit Gewichten $w_i$
Gesucht: $L$ Partikel mit Geweichte $\frac{1}{L}$ (gleichgewichtet)
Sequential Importance Sampling
$f_{k}^{e}\left(\underline{x}_{k}\right)=f\left(\underline{x}_{k} \mid \underline{y}_{1: k}\right)$ auf $\underline{x}_{1: k-1}$ marginalisieren
$$ f_{k}^{e}\left(\underline{x}_{k}\right)=f\left(\underline{x}_{k} \mid \underline{y}_{1: k}\right)=\int_{\mathbb{R}^{N}} \cdots \int_{\mathbb{R}^{N}} f\left(\underline{x}_{1: k} \mid \underline{y}_{1 : k}\right) d \underline{x}_{1: k-1} $$Importance Sampling für $f(\underline{x}_k, \underline{x}_{k-1} \mid \underline{y}_{1:k})$
$$ f_{k}^{e}\left(\underline{x}_{k}\right) = \int_{\mathbb{R}^{N}} \cdots \int_{\mathbb{R}^{N}} \underbrace{\frac{f\left(\underline{x}_{1: k} \mid \underline{y}_{1 : k}\right)}{p\left(\underline{x}_{1: k} \mid \underline{y}_{1 : k}\right)}}_{=: w_k^{e, i}} p\left(\underline{x}_{1: k} \mid \underline{y}_{1 : k}\right) d \underline{x}_{1: k-1} $$$\frac{f\left(\underline{x}_{1: k} \mid \underline{y}_{1 : k}\right)}{p\left(\underline{x}_{1: k} \mid \underline{y}_{1 : k}\right)}$ umschreiben
Zähler
$$ \begin{aligned} f\left(\underline{x}_{1: k} \mid \underline{y}_{1: k}\right) &\propto f\left(\underline{y}_{k} \mid \underline{x}_{1: k}, \underline{y}_{1: k - 1}\right) \cdot f\left(\underline{x}_{1: k} \mid \underline{y}_{1: k-1}\right)\\ &=f\left(\underline{y}_{k} \mid \underline{x}_{k}\right) \cdot f\left(\underline{x}_{k} \mid \underline{x}_{1:k-1}, \underline{y}_{1:k-1}\right) \cdot f\left(\underline{x}_{1:k-1} \mid \underline{y}_{1: k-1}\right)\\ &=f\left(\underline{y}_{k} \mid \underline{x}_{k}\right) \cdot f\left(\underline{x}_{k} \mid \underline{x}_{k-1}\right) \cdot f\left(\underline{x}_{1: k-1} \mid \underline{y}_{1: k \cdot 1}\right) \end{aligned} $$Nenner
$$ p\left(\underline{x}_{1: k} \mid \underline{y}_{1: k}\right)=p\left(\underline{x}_{k} \mid \underline{x}_{1: k - 1}, \underline{y}_{1: k}\right) \cdot p\left(\underline{x}_{1: k -1} \mid \underline{y}_{1: k - 1}\right) $$
Einsetzen, $w_k^{e, i}$ in Rekursiven Form schreiben
$$ w_k^{e, i} = \frac{f\left(\underline{\hat{x}}_{1: k} \mid \underline{y}_{1 : k}\right)}{p\left(\underline{\hat{x}}_{1: k} \mid \underline{y}_{1 : k}\right)} \propto \frac{f\left(\underline{y}_{k} \mid \underline{x}_{k}^i\right) \cdot f\left(\underline{x}_{k}^i\mid \underline{x}_{k-1}^i\right)}{p\left(\underline{x}_{k}^i \mid \underline{x}_{1: k - 1}^i, \underline{y}_{1: k}\right)} \cdot \underbrace{\frac{f\left(\underline{x}_{1: k-1}^i \mid \underline{y}_{1: k \cdot 1}\right)}{p\left(\underline{x}_{1: k -1}^i \mid \underline{y}_{1: k - 1}\right)}}_{=w_{k-1}^{e, i}} $$und Normalisieren.
Spezielle Proposals
Standard Proposal
$$ p\left(\underline{x}_{k} \mid \underline{x}_{k-1}, \underline{y}_{k}\right) \stackrel{!}{=} f\left(\underline{x}_{k} \mid \underline{x}_{k-1}\right) $$Dann ist
$$ w_{k}^{e, i} \propto \frac{f\left(\underline{y}_{k} \mid \hat{\underline{x}}_{k}^{i}\right) \cdot f\left(\hat{\underline{x}}_{k}^{i} \mid \hat{\underline{x}}_{k-1}^{i}\right)}{p\left(\underline{\hat{x}}_{k}^{i} \mid \hat{\underline{x}}_{k-1}^{i}, \underline{y}_k\right)} \cdot w_{k-1}^{e, i}=f\left(\underline{y}_{k} \mid \hat{\underline{x}}_{k}^{i}\right) \cdot w_{k - 1}^{e, i} $$Sehr einfach aber keine verbesserte Performance.
Optimales Proposal
$$ \begin{aligned} p\left(\underline{x}_{k} \mid \underline{x}_{k-1}, \underline{y}_{k}\right) &=f\left(\underline{x}_{k} \mid \underline{x}_{k-1}, \underline{y}_{k}\right) \\ & \propto f\left(\underline{y}_{k} \mid \underline{x}_{k}\right) \cdot f\left(\underline{x}_{k} \mid \underline{x}_{k-1}\right) \end{aligned} $$Dann ist
$$ w_k^{e, i} = w_{k-1}^{e, i} $$Minimierte Varianz der Gewichte aber nur in Spezialfällen verwendbar.