Prädiktion nichtlinearer Systeme Chapman-Kolmogorov-Gleichung Verbunddichte
f ( x ‾ k + 1 , x ‾ k ) = f ( x ‾ k + 1 ∣ x ‾ k ) ⋅ f ( x ‾ k )
f\left(\underline{x}_{k+1}, \underline{x}_{k}\right)=f\left(\underline{x}_{k+1} \mid \underline{x}_{k}\right) \cdot f\left(\underline{x}_{k}\right)
f ( x k + 1 , x k ) = f ( x k + 1 ∣ x k ) ⋅ f ( x k ) Marginalisierung
f ( x k + 1 ) = ∫ R N f ( x ‾ k + 1 ∣ x ‾ k ) ⋅ f ( x ‾ k ) d x ‾ k
f\left(x_{k+1}\right)=\int_{\mathbb{R}^{N}} f\left(\underline{x}_{k+1} \mid \underline{x}_{k}\right) \cdot f\left(\underline{x}_{k}\right) d \underline{x}_{k}
f ( x k + 1 ) = ∫ R N f ( x k + 1 ∣ x k ) ⋅ f ( x k ) d x k Definition
Prädiktion für dynamische Systeme ( Chapman-Kolmogorov-Gleichung
f k + 1 p ( x ‾ k + 1 ) = ∫ R N f ( x ‾ k + 1 ∣ x ‾ k ) ⏟ Pr a ¨ diktionsdichte f k e ( x ‾ k ) d x ‾ k
f_{k+1}^{p}\left(\underline{x}_{k+1}\right)=\int_{\mathbb{R}^{N}} \underbrace{f\left(\underline{x}_{k+1} \mid \underline{x}_{k}\right)}_{\text{Prädiktionsdichte}} f_{k}^{e}\left(\underline{x}_{k}\right) \mathrm{d} \underline{x}_{k}
f k + 1 p ( x k + 1 ) = ∫ R N Pr a ¨ diktionsdichte f ( x k + 1 ∣ x k ) f k e ( x k ) d x k Erklärung Die Chapman-Kolmogorov-Gleichung berechnet die Dichte von x ‾ k + 1 \underline{x}_{k+1} x k + 1 Dichte f k e ( x ‾ k ) f_{k}^{e}\left(\underline{x}_{k}\right) f k e ( x k ) x ‾ k \underline{x}_{k} x k f ( x ‾ k + 1 ∣ x ‾ k ) f\left(\underline{x}_{k+1} \mid \underline{x}_{k}\right) f ( x k + 1 ∣ x k ) x ‾ k + 1 \underline{x}_{k+1} x k + 1 konkreten Wert von x ‾ k \underline{x}_{k} x k
Problem ‼️ Es handelt sich um ein Parameterintegral!
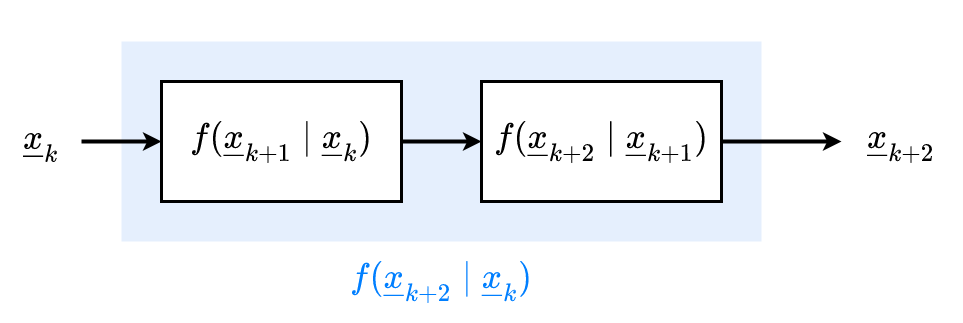
Integrand hängt von x ‾ k + 1 \underline{x}_{k+1} x k + 1 Nur möglich für analytische Lösung Sonst erfordert (numerische) Lösung des Integrals für alle x ‾ k + 1 \underline{x}_{k+1} x k + 1 f ( x ‾ k + 2 , x ‾ k ) = ∫ R N f ( x ‾ k + 2 , x ‾ k + 1 , x ‾ k ) d x ‾ k + 1 f ( x ‾ k + 2 ∣ x ‾ k ) f ( x ‾ k ) = ∫ R N f ( x ‾ k + 2 ∣ x ‾ k + 1 , x ‾ k ) f ( x ‾ k + 1 , x ‾ k ) d x ‾ k + 1 ∣ Markov f ( x ‾ k + 2 ∣ x ‾ k ) f ( x ‾ k ) = ∫ R N f ( x ‾ k + 2 ∣ x ‾ k + 1 ) f ( x ‾ k + 1 , x ‾ k ) d x ‾ k + 1 f ( x ‾ k + 2 ∣ x ‾ k ) f ( x ‾ k ) = ∫ R N f ( x ‾ k + 2 ∣ x ‾ k + 1 ) f ( x ‾ k + 1 ∣ x ‾ k ) f ( x ‾ k ) d x ‾ k + 1 f ( x ‾ k + 2 ∣ x ‾ k ) = ∫ R N f ( x ‾ k + 2 ∣ x ‾ k + 1 ) f ( x ‾ k + 1 ∣ x ‾ k ) d x ‾ k + 1
\begin{aligned}
f(\underline{x}_{k + 2}, \underline{x}_{k}) &= \int_{\mathbb{R}^N} f(\underline{x}_{k+2}, \underline{x}_{k+1}, \underline{x}_{k}) d\underline{x}_{k+1} \\\\
f(\underline{x}_{k + 2} \mid \underline{x}_{k}) f(\underline{x}_{k}) &= \int_{\mathbb{R}^N} f(\underline{x}_{k+2} \mid \underline{x}_{k+1}, \underline{x}_{k}) f(\underline{x}_{k+1}, \underline{x}_{k}) d\underline{x}_{k+1} \quad | \quad \text{Markov} \\\\
f(\underline{x}_{k + 2} \mid \underline{x}_{k}) f(\underline{x}_{k}) &= \int_{\mathbb{R}^N} f(\underline{x}_{k+2} \mid \underline{x}_{k+1}) f(\underline{x}_{k+1}, \underline{x}_{k}) d\underline{x}_{k+1} \\\\
f(\underline{x}_{k + 2} \mid \underline{x}_{k}) f(\underline{x}_{k}) &= \int_{\mathbb{R}^N} f(\underline{x}_{k+2} \mid \underline{x}_{k+1}) f(\underline{x}_{k+1} \mid \underline{x}_{k}) f(\underline{x}_{k})d\underline{x}_{k+1} \\\\
f(\underline{x}_{k + 2} \mid \underline{x}_{k}) &= \int_{\mathbb{R}^N} f(\underline{x}_{k+2} \mid \underline{x}_{k+1}) f(\underline{x}_{k+1} \mid \underline{x}_{k}) d\underline{x}_{k+1}
\end{aligned}
f ( x k + 2 , x k ) f ( x k + 2 ∣ x k ) f ( x k ) f ( x k + 2 ∣ x k ) f ( x k ) f ( x k + 2 ∣ x k ) f ( x k ) f ( x k + 2 ∣ x k ) = ∫ R N f ( x k + 2 , x k + 1 , x k ) d x k + 1 = ∫ R N f ( x k + 2 ∣ x k + 1 , x k ) f ( x k + 1 , x k ) d x k + 1 ∣ Markov = ∫ R N f ( x k + 2 ∣ x k + 1 ) f ( x k + 1 , x k ) d x k + 1 = ∫ R N f ( x k + 2 ∣ x k + 1 ) f ( x k + 1 ∣ x k ) f ( x k ) d x k + 1 = ∫ R N f ( x k + 2 ∣ x k + 1 ) f ( x k + 1 ∣ x k ) d x k + 1 Prädiktion mit CK-Glg.: Lösungsansätze Im allgemeinen Fall ist CK-Gleichung NICHT exakt lösbar 🤪
Ausnahme (Bsp.)
Vereinfachte Prädiktion Systemmodell mit additivem Rauschen Wir beginnen mit additivem Rauschen.
Generatives Modell
x ‾ k + 1 = a ‾ k ( x ‾ k ) + w ‾ k x ‾ k + 1 , x ‾ k , w ‾ k ∈ R N
\underline{x}_{k+1} = \underline{a}_{k}(\underline{x}_{k}) + \underline{w}_{k} \qquad \underline{x}_{k+1}, \underline{x}_{k}, \underline{w}_{k} \in \mathbb{R}^N
x k + 1 = a k ( x k ) + w k x k + 1 , x k , w k ∈ R N Vereinfachte Schreibweise
z ‾ = a ‾ ( x ‾ ) + w ‾
\underline{z} = \underline{a}(\underline{x}) + \underline{w}
z = a ( x ) + w Probablistisches Modell (inkl. Rauschen)
f ( z ‾ ∣ x ‾ ) = f w ( z ‾ − a ‾ ( x ‾ ) )
f(\underline{z} \mid \underline{x}) = f_w(\underline{z} - \underline{a}(\underline{x}))
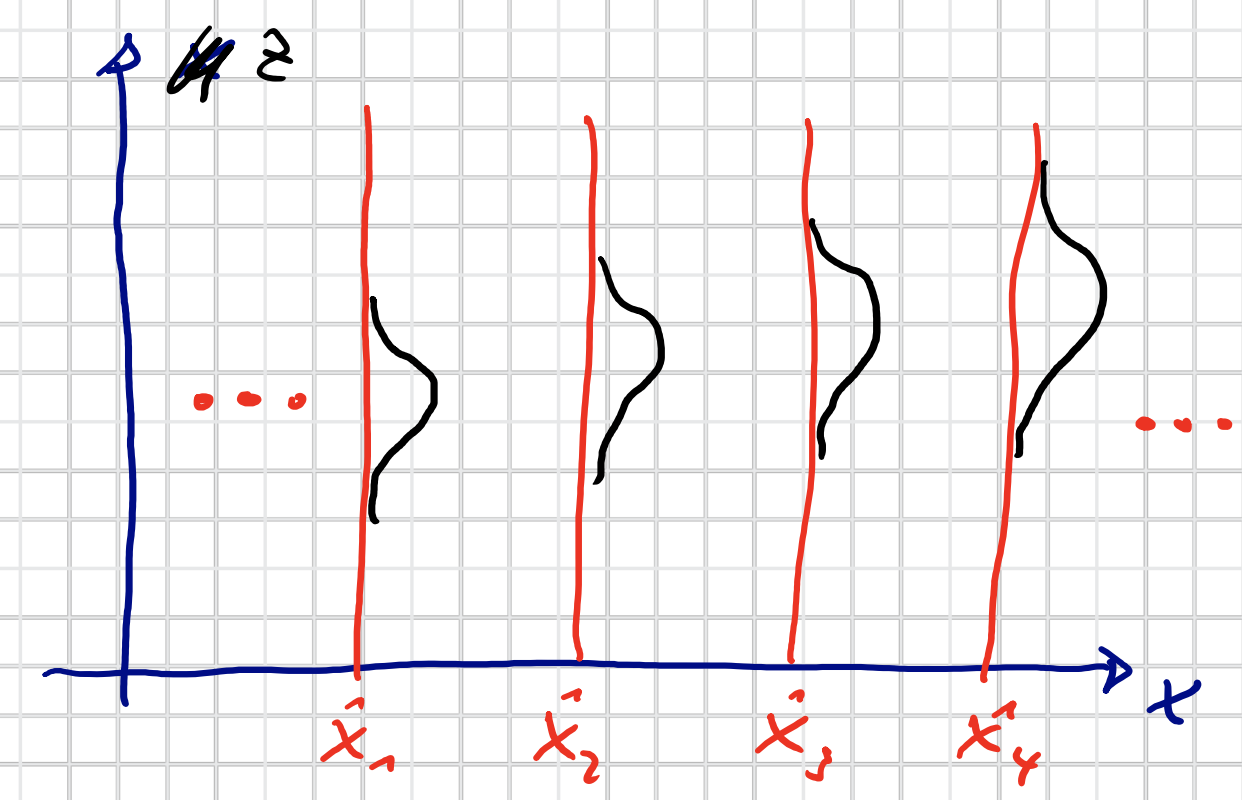
f ( z ∣ x ) = f w ( z − a ( x )) Vereinfachung: Aufteilung in diskrete “Streifen”:
f ( z ‾ ∣ x ^ ‾ i ) = f w ( z ‾ − a ‾ ( x ^ ‾ i ) ) i ∈ Z
f\left(\underline{z} \mid \underline{\hat{x}}_{i}\right)=f_w\left(\underline{z}-\underline{a}\left(\underline{\hat{x}}_{i}\right)\right) \qquad i \in \mathbb{Z}
f ( z ∣ x ^ i ) = f w ( z − a ( x ^ i ) ) i ∈ Z In den “Zwischenräumen” gilt nun aber ∫ f ( z ‾ ∣ x ‾ ) = 1 \int f(\underline{z} \mid \underline{x}) = 1 ∫ f ( z ∣ x ) = 1 f i ( x ‾ ) f_i(\underline{x}) f i ( x )
f i ( x ‾ ) = N ( x ‾ , x ^ ‾ i , C i ) i ∈ Z
f_i(\underline{x}) = \mathcal{N}(\underline{x}, \underline{\hat{x}}_i, C_i) \qquad i \in \mathbb{Z}
f i ( x ) = N ( x , x ^ i , C i ) i ∈ Z mit
f ( x ‾ ) = ∑ i ∈ Z w i f i ( x ‾ ) ≈ 1
f(\underline{x}) = \sum_{i \in \mathbb{Z}} w_if_i(\underline{x}) \approx 1
f ( x ) = i ∈ Z ∑ w i f i ( x ) ≈ 1 Z.B. Skalarer Fall
> f ( x ) = ∑ i ∈ Z w i f i ( x ) , f i ( x ) = exp ( − 1 2 ( x − x ^ i ) 2 σ 2 ) >
> f(x)=\sum_{i \in \mathbb{Z}} w_{i} f_i(x), \quad f_i(x)=\exp \left(-\frac{1}{2} \frac{\left(x-\hat{x}_{i}\right)^{2}}{\sigma^{2}}\right)
> > f ( x ) = i ∈ Z ∑ w i f i ( x ) , f i ( x ) = exp ( − 2 1 σ 2 ( x − x ^ i ) 2 ) > mit geeigneten σ \sigma σ
Betrachtung für jeweils ein Komponente i i i
f i ( z ‾ ∣ x ‾ ) = f ( z ‾ ∣ x ^ ‾ i ) ⋅ f i ( x ‾ )
f_i(\underline{z} \mid \underline{x}) = f(\underline{z} \mid \underline{\hat{x}}_i) \cdot f_i(\underline{x})
f i ( z ∣ x ) = f ( z ∣ x ^ i ) ⋅ f i ( x ) Gesamtdichte ist
f ( z ‾ ∣ x ‾ ) ≈ ∑ i ∈ Z w i f ( z ‾ ∣ x ^ ‾ i ) ⋅ f i ( x ‾ )
f(\underline{z} \mid \underline{x}) \approx \sum_{i \in \mathbb{Z}} w_i f(\underline{z} \mid \underline{\hat{x}}_i) \cdot f_i(\underline{x})
f ( z ∣ x ) ≈ i ∈ Z ∑ w i f ( z ∣ x ^ i ) ⋅ f i ( x ) Es gilt
∫ R N f ( z ‾ ( x ‾ ) d z ‾ = ∑ i ∈ Z w i f i ( x ‾ ) ∫ R N f ( z ‾ ∣ x ‾ ) d z ‾ ⏟ = 1 = ∑ i ∈ Z w i f i ( x ‾ ) ≈ 1
\begin{aligned}
\int_{\mathbb{R}^{N}} f(\underline{z}(\underline{x}) d \underline{z}&=\sum_{i \in \mathbb{Z}} w_{i} f_{i}(\underline{x}) \underbrace{\int_{\mathbb{R}^N}f(\underline{z} \mid \underline{x}) d\underline{z}}_{=1}\\
&=\sum_{i \in \mathbb{Z}} w_{i} f_{i}(\underline{x}) \approx 1
\end{aligned}
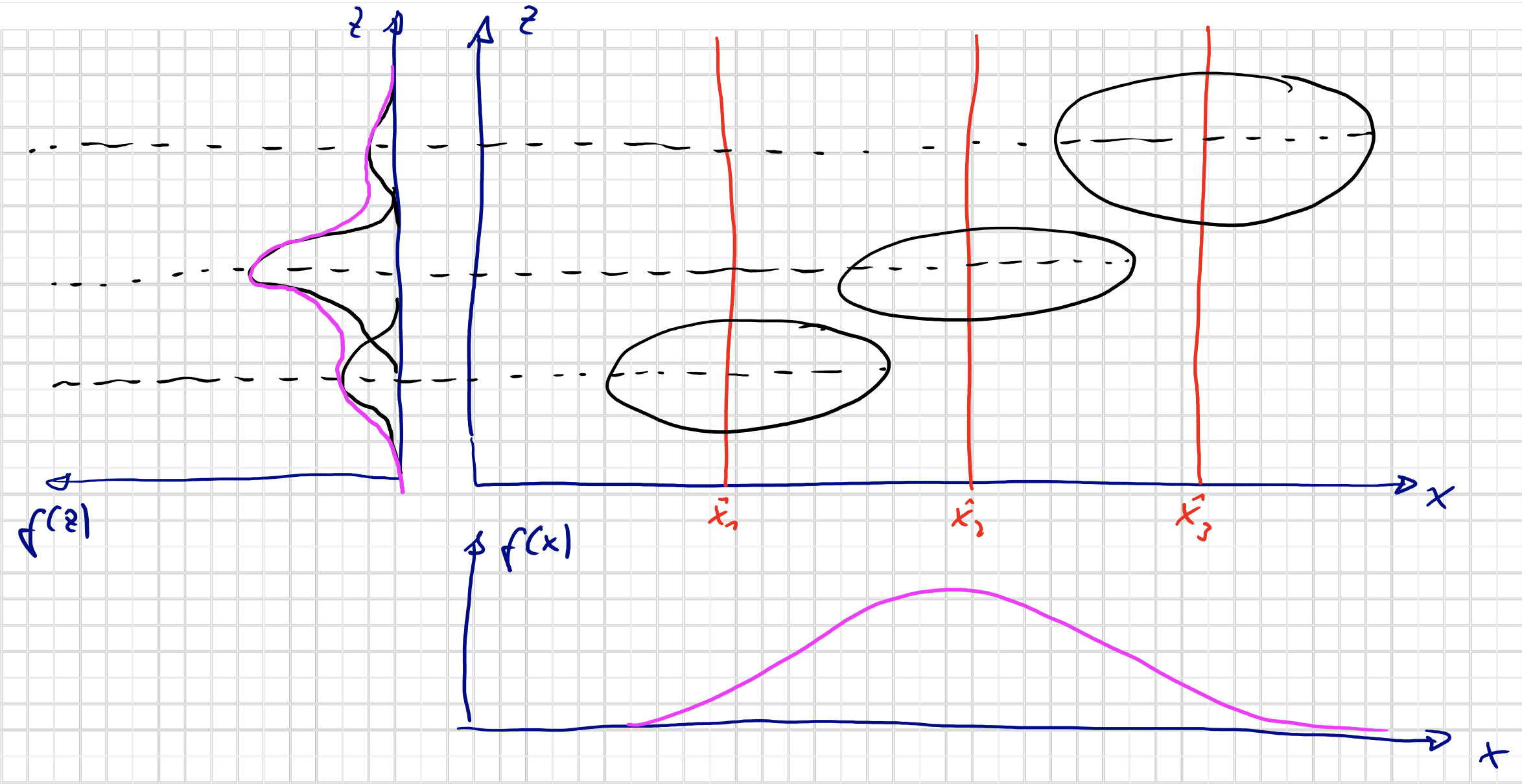
∫ R N f ( z ( x ) d z = i ∈ Z ∑ w i f i ( x ) = 1 ∫ R N f ( z ∣ x ) d z = i ∈ Z ∑ w i f i ( x ) ≈ 1 Fall Rauschen w ‾ k \underline{w}_k w k f ( z ‾ ∣ x ‾ ) f(\underline{z} \mid \underline{x} ) f ( z ∣ x )
f ( z ‾ ∣ x ‾ ) = ∑ i ∈ Z f i z ( z ‾ ) ⏟ f w ( z ‾ − a ‾ ( x ^ ‾ i ) ) ⋅ f i x ( x ‾ )
f(\underline{z} \mid \underline{x}) = \sum_{i \in \mathbb{Z}} \underbrace{f_i^z(\underline{z})}_{f_w(\underline{z} - \underline{a}(\underline{\hat{x}}_i))} \cdot f_i^x(\underline{x})
f ( z ∣ x ) = i ∈ Z ∑ f w ( z − a ( x ^ i )) f i z ( z ) ⋅ f i x ( x ) Allgemeine Systemmodelle x ‾ k + 1 = a ‾ k ( x ‾ k , w ‾ k )
\underline{x}_{k+1} = \underline{a}_k (\underline{x}_k, \underline{w}_k)
x k + 1 = a k ( x k , w k ) Vereinfachte Schreibweise:
z ‾ = a ‾ ( x ‾ , w ‾ )
\underline{z} = \underline{a}(\underline{x}, \underline{w})
z = a ( x , w ) Ergibt allgemeine Transitionsdichte f ( z ‾ ∣ x ‾ ) f(\underline{z} | \underline{x}) f ( z ∣ x )
f ( z ‾ ∣ x ‾ ) = ∑ i ∈ Z w i f i z ( z ‾ ) ⋅ f i x ( x ‾ )
f(\underline{z} | \underline{x}) = \sum_{i \in \mathbb{Z}} w_i f_i^z(\underline{z}) \cdot f_i^x(\underline{x})
f ( z ∣ x ) = i ∈ Z ∑ w i f i z ( z ) ⋅ f i x ( x ) Wichtig ist, dass die einzelnen Komponenten entkoppelt sind. 👏
Bsp 1 Annahme: f ( x ‾ ) f(\underline{x}) f ( x )
Einsetzen in CK-Gleichung:
f ( z ‾ ) = ∫ R N ( ∑ i ∈ Z w i f i z ( z ‾ ) ⋅ f i x ( x ‾ ) ) f ( x ‾ ) d x ‾ = ∑ i ∈ Z w i f i z ( z ‾ ) ∫ R N f i x ( x ‾ ) ⋅ f ( x ‾ ) d x ‾ ⏟ Konstante c i = ∑ i ∈ Z w i c i ⏟ = : w ˉ i f i z ( z ‾ ) = ∑ i ∈ Z w ˉ i f i z ( z ‾ )
\begin{aligned}
f(\underline{z})&=\int_{\mathbb{R}^{N}}\left(\sum_{i \in \mathbb{Z}} w_{i} f_{i}^{z}(\underline{z}) \cdot f_{i}^{x}(\underline{x})\right) f(\underline{x}) d \underline{x}\\
&=\sum_{i \in \mathbb{Z}} w_{i} f_{i}^{z}(\underline{z}) \underbrace{\int_{\mathbb{R}^{N}} f_{i}^{x}(\underline{x}) \cdot f(\underline{x}) d \underline{x}}_{\text{Konstante } c_{i}}\\
&= \sum_{i \in \mathbb{Z}} \underbrace{w_{i} c_i}_{=: \bar{w}_i} f_{i}^{z}(\underline{z})\\
&=\sum_{i \in \mathbb{Z}} \bar{w}_{i} f_{i}^{z}(\underline{z})
\end{aligned}
f ( z ) = ∫ R N ( i ∈ Z ∑ w i f i z ( z ) ⋅ f i x ( x ) ) f ( x ) d x = i ∈ Z ∑ w i f i z ( z ) Konstante c i ∫ R N f i x ( x ) ⋅ f ( x ) d x = i ∈ Z ∑ =: w ˉ i w i c i f i z ( z ) = i ∈ Z ∑ w ˉ i f i z ( z ) Hier sieht man, dass f i z ( z ‾ ) f_i^z(\underline{z}) f i z ( z ) x ‾ \underline{x} x
Speizialfall: f ( x ‾ ) = δ ( x ‾ − x ^ ‾ ) ⇒ f(\underline{x}) = \delta(\underline{x} - \underline{\hat{x}}) \Rightarrow f ( x ) = δ ( x − x ^ ) ⇒
c i = ∫ R N f i ( x ‾ ) δ ( x ‾ − x ^ ‾ ) d x ‾ = f i ( x ^ ‾ )
c_i = \int_{\mathbb{R}^{N}} f_{i}(\underline{x}) \delta \left(\underline{x}-\underline{\hat{x}}\right) d \underline{x}=f_i(\underline{\hat{x}})
c i = ∫ R N f i ( x ) δ ( x − x ^ ) d x = f i ( x ^ ) Bsp 2 Annahme: Gaussian Mixture
f ( x ‾ ) = ∑ j = 1 L v j f j ∗ ( x ‾ )
f(\underline{x}) = \sum_{j=1}^L v_j f_j^*(\underline{x})
f ( x ) = j = 1 ∑ L v j f j ∗ ( x ) Einsetzen in CK-Gleichung:
f ( z ‾ ) = ∫ R N { ∑ i ∈ Z w i f i z ( z ‾ ) f i x ( x ‾ ) } ⋅ { ∑ i = 1 L v j f j ∗ ( x ‾ ) } d x = ∑ i ∈ Z w i f i z ( z ‾ ) ∑ i = 1 L v j ∫ R N f i x ( x ‾ ) ⋅ f j ∗ ( x ‾ ) d x ‾ ⏟ Konstante ⏟ Kondante C i = ∑ i ∈ π w i C i ⏟ = : w ˉ i f i z ( z ‾ ) = ∑ i ∈ π w ˉ i f i z ( z ‾ )
\begin{aligned}
f(\underline{z})&=\int_{\mathbb{R}^{N}}\left\{\sum_{i \in \mathbb{Z}} w_{i} f_{i}^{z}(\underline{z}) f_{i}^{x}(\underline{x})\right\} \cdot \left\{\sum_{i=1}^{L} v_{j} f_{j}^{*}(\underline{x})\right\} d x\\
&=\sum_{i \in \mathbb{Z}} w_{i} f_{i}^{z}(\underline{z}) \underbrace{\sum_{i=1}^{L} v_{j} \underbrace{\int_{\mathbb{R}^N} f_{i}^{x}(\underline{x}) \cdot f_{j}^{*}(\underline{x}) d \underline{x}}_{\text{Konstante}}}_{\text {Kondante } C_{i}} \\
&=\sum_{i \in \pi} \underbrace{w_{i}C_i}_{=: \bar{w}_i} f_{i}^{z}(\underline{z}) \\
&=\sum_{i \in \pi} \bar{w}_{i} f_{i}^{z}(\underline{z})
\end{aligned}
f ( z ) = ∫ R N { i ∈ Z ∑ w i f i z ( z ) f i x ( x ) } ⋅ { i = 1 ∑ L v j f j ∗ ( x ) } d x = i ∈ Z ∑ w i f i z ( z ) Kondante C i i = 1 ∑ L v j Konstante ∫ R N f i x ( x ) ⋅ f j ∗ ( x ) d x = i ∈ π ∑ =: w ˉ i w i C i f i z ( z ) = i ∈ π ∑ w ˉ i f i z ( z )